
【题目】某公司计划种植A,B两种中药材,该公司最多能承包50亩的土地,可使用的周转资金不超过54万元,假设药材A售价为0.55万元/吨,产量为4吨/亩,种植成本1.2万元/亩;药材B售价为0.3万元/吨,产量为6吨/亩,种植成本0.9万元/亩时公司的总利润最大,则A,B两种中药材的种植面积应各为多少亩,最大利润为多少万元?
【答案】解:设A,B两种中药材的种植面积各x亩,y亩;
则由题意可得,  ;即:
;即: 
一年的种植总利润z=0.55×4x+0.3×6y﹣(1.2x+0.9y)=x+0.9y万元;
作平面区域如下,
结合图象可知,![]() ;
;
解得,x=30,y=20;此时一年的种植总利润最大;
那么A药材的面积是30亩;B药材的面积为20亩,
此时利润的最大值为:Z=30+0.9×20=48万元.
故答案为:A药材的面积是30亩;B药材的面积为20亩,利润的最大值为48万元.
【解析】由题意,设A,B两种中药材的种植面积各x亩,y亩;从而可得约束条件,一年的种植总利润z=0.55×4x+0.3×6y﹣(1.2x+0.9y)=x+0.9y;从而由线性规划求最优解即可.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=3,a2=5,其前n项和为Sn满足Sn+Sn﹣2=2Sn﹣1+2n﹣1(n≥3,n∈N*)
(1)试求数列{an}的通项公式
(2)令bn= ![]() ,Tn是数列{bn}的前n项和.证明:对任意给定的m∈(0,
,Tn是数列{bn}的前n项和.证明:对任意给定的m∈(0, ![]() ),均存在n0∈N*,使得当n≥n0时,Tn>m恒成立.
),均存在n0∈N*,使得当n≥n0时,Tn>m恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列结论:
①在△ABC中,sinA>sinBa>b;
②常数数列既是等差数列又是等比数列;
③数列{an}的通项公式为 ![]() ,若{an}为递增数列,则k∈(﹣∞,2];
,若{an}为递增数列,则k∈(﹣∞,2];
④△ABC的内角A,B,C满足sinA:sinB:sinC=3:5:7,则△ABC为锐角三角形.其中正确结论的个数为( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品分为 ![]() 三级,若生产中出现
三级,若生产中出现 ![]() 级品的概率为0.03,出现
级品的概率为0.03,出现 ![]() 级品的概率为0.01,则对产品抽查一次抽得
级品的概率为0.01,则对产品抽查一次抽得 ![]() 级品的概率是( )
级品的概率是( )
A.0.09
B.0.98
C.0.97
D.0.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,给出的是计算1+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() 的值的一个程序框图,判断框内应填入的条件是( )
的值的一个程序框图,判断框内应填入的条件是( ) 
A.i<101?
B.i>101?
C.i≤101?
D.i≥101?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上. 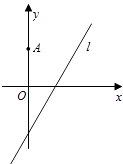
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100] 
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com