
【题目】在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.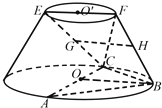
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB= ![]() AC=2
AC=2 ![]() AB=BC,求二面角F﹣BC﹣A的余弦值.
AB=BC,求二面角F﹣BC﹣A的余弦值.
【答案】
(1)
证明:取FC中点Q,连结GQ、QH,
∵G、H为EC、FB的中点,
∴GQ ![]()
![]() ,QH
,QH![]()
![]() ,又∵EF
,又∵EF ![]() BO,∴GQ
BO,∴GQ ![]()
![]() BO,
BO,
∴平面GQH∥平面ABC,
∵GH面GQH,∴GH∥平面ABC
(2)
解:

∵AB=BC,∴BO⊥AC,
又∵OO′⊥面ABC,
∴以O为原点,OA为x轴,OB为y轴,OO′为z轴,建立空间直角坐标系,
则A(2 ![]() ,0,0),C(﹣2
,0,0),C(﹣2 ![]() ,0,0),B(0,2
,0,0),B(0,2 ![]() ,0),O′(0,0,3),F(0,
,0),O′(0,0,3),F(0, ![]() ,3),
,3),
![]() =(﹣2
=(﹣2 ![]() ,﹣
,﹣ ![]() ,﹣3),
,﹣3), ![]() =(2
=(2 ![]() ,2
,2 ![]() ,0),
,0),
由题意可知面ABC的法向量为 ![]() =(0,0,3),
=(0,0,3),
设 ![]() =(x0,y0,z0)为面FCB的法向量,
=(x0,y0,z0)为面FCB的法向量,
则  ,即
,即 ![]() ,
,
取x0=1,则 ![]() =(1,﹣1,﹣
=(1,﹣1,﹣ ![]() ),
),
∴cos< ![]() ,
, ![]() >=
>=  =
= ![]() =﹣
=﹣ ![]() .
.
∵二面角F﹣BC﹣A的平面角是锐角,
∴二面角F﹣BC﹣A的余弦值为 ![]() .
.
【解析】(1)取FC中点Q,连结GQ、QH,推导出平面GQH∥平面ABC,由此能证明GH∥平面ABC.(2)由AB=BC,知BO⊥AC,以O为原点,OA为x轴,OB为y轴,OO′为z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣BC﹣A的余弦值.;本题考查线面平行的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是等比数列,且b2=3,b3=9,a1=b1 , a14=b4 .
(1)求{an}的通项公式;
(2)设cn=an+bn , 求数列{cn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,其中a>0且a≠1,若a=
,其中a>0且a≠1,若a=![]() 时方程f(x)=b有两个不同的实根,则实数b的取值范围是______;若f(x)的值域为[3,+∞],则实数a的取值范围是______.
时方程f(x)=b有两个不同的实根,则实数b的取值范围是______;若f(x)的值域为[3,+∞],则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=a(x﹣lnx)+ ![]() ,a∈R.
,a∈R.
(1)讨论f(x)的单调性;
(2)当a=1时,证明f(x)>f′(x)+ ![]() 对于任意的x∈[1,2]成立.
对于任意的x∈[1,2]成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在圆锥PO中,已知![]() ,圆O的直径
,圆O的直径![]() ,C是弧AB的中点,D为AC的中点.
,C是弧AB的中点,D为AC的中点.

(1)求异面直线PD和BC所成的角的正切值;
(2)求直线OC和平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcos θ=4.
(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;
(2)设点A的极坐标为![]() ,点B在曲线C2上,求△OAB面积的最大值.
,点B在曲线C2上,求△OAB面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com