
【题目】已知点F为抛物线C:x2=2py (p>0) 的焦点,点A(m,3)在抛物线C上,且|AF|=5,若点P是抛物线C上的一个动点,设点P到直线![]() 的距离为
的距离为![]() ,设点P到直线
,设点P到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线C的方程;
(2) 求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知正方体ABCD-A1B1C1D1的棱长为a,点E,F,G分别为棱AB,AA1,C1D1的中点.下列结论中,正确结论的序号是______.
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②B1D1∥平面EFG;
③BD1⊥平面ACB1;
④异面直线EF与BD1所成角的正切值为![]() ;
;
⑤四面体ACB1D1的体积等于![]() a3
a3

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,其中
,其中![]() ,
, ![]() 为左、右焦点,且离心率
为左、右焦点,且离心率![]() ,直线
,直线![]() 与椭圆交于两不同点
与椭圆交于两不同点![]() ,
, ![]() .当直线
.当直线![]() 过椭圆
过椭圆![]() 右焦点
右焦点![]() 且倾斜角为
且倾斜角为![]() 时,原点
时,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395913728/STEM/2d7d70ba831f438cb4e191e234d85c18.png]
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,当
,当![]() 面积为
面积为![]() 时,求
时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x-a|-![]() x(a>0).
x(a>0).
(1)若a=3,解关于x的不等式f(x)<0;
(2)若对于任意的实数x,不等式f(x)-f(x+a)<a2+![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了探究某市高中理科生在高考志愿中报考“经济类”专业是否与性别有关,现从该市高三理科生中随机抽取50名学生进行调查,得到如下2×2列联表:(单位:人)

(1)据此样本,判断能否在犯错误的概率不超过0.001的前提下认为理科生报考“经济类”专业与性别有关?
(2)若以样本中各事件的频率作为概率估计全市总体考生的报考情况,现从该市的全体考生(人数众多)中随机抽取3人,设3人中报考“经济类”专业的人数为随机变量X,求随机变量X的概率分布列及数学期望.
附:
![]()
![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在2013年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.

(1)求出第4组的频率,并补全频率分布直方图;
(2)根据样本频率分布直方图估计样本的中位数与平均数;
(3)如果用分层抽样的方法从“优秀”和“良好”的学生中共选出5人,再从这5人中选2人,那么至少有一人是“优秀”的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD中,边长为2,E为AB中点,F是边BC上的动点.
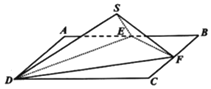
(1)将△ADE沿DE翻折90°到△SDE,求二面角S-DC-E的正切值;
(2)若![]() ,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求
,将△ADE沿DE翻折到△SDE,△BEF沿EF翻折到△SEF,接DF,设直线DS与平面DEF所成角为θ,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com