
【题目】已知函数f(x)是二次函数,且满足f(0)=1,f(x+1)﹣f(x)=2x+5;函数g(x)=ax(a>0且a≠1)
(1)求f(x)的解析式;
(2)若g(2)= ![]() ,且g[f(x)]≥k对x∈[﹣1,1]恒成立,求实数k的取值范围.
,且g[f(x)]≥k对x∈[﹣1,1]恒成立,求实数k的取值范围.
【答案】
(1)解:∵f(x+1)﹣f(x)=2x+5,
∴f(1)﹣f(0)=5,f(2)﹣f(1)=7,
又f(0)=1,∴f(1)=6,f(2)=13.
设f(x)=mx2+bx+c,
则 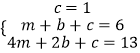 ,解得m=1,b=4.
,解得m=1,b=4.
∴f(x)=x2+4x+1
(2)解:∵g(2)=a2= ![]() ,∴a=
,∴a= ![]() .
.
∴g[f(x)]=( ![]() )
) ![]() ,
,
∵f(x)=x2+4x+1在[﹣1,1]上单调递增,g(x)是减函数,
∴g(f(x))在[﹣1,1]上是减函数,
g(f(x))在[﹣1,1]上的最小值为g(f(1))=g(6)= ![]() =
= ![]() .
.
∵g[f(x)]≥k对x∈[﹣1,1]恒成立,
∴k≤ ![]()
【解析】(1)利用关系式求出f(1),f(2),利用待定系数法求出f(x);(2)求出a的值,判断g(f(x))的单调性,根据单调性得出g(f(x))在[﹣1,1]上的最小值,从而得出k的范围.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在封闭的直三棱柱ABC﹣A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=5,则V的最大值是( )
A.4π
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣ ![]() x+c(a,c∈R)满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0
x+c(a,c∈R)满足条件:①f(1)=0;②对一切x∈R,都有f(x)≥0
(1)求a、c的值;
(2)若存在实数m,使函数g(x)=f(x)﹣mx在区间[m,m+2]上有最小值﹣5,求出实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A是△BCD所在平面外一点,M、N为△ABC和△ACD重心,BD=6; 
(1)求MN的长;
(2)若A、C的位置发生变化,MN的位置和长度会改变吗?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅装修,需要大块胶合板![]() 张,小块胶合板
张,小块胶合板![]() 张,已知市场出售
张,已知市场出售![]() 两种不同规格的胶合板。经过测算,
两种不同规格的胶合板。经过测算, ![]() 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板![]() 张,小块胶合板
张,小块胶合板![]() 张,
张, ![]() 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板![]() 张,小块胶合板
张,小块胶合板![]() 张.已知
张.已知![]() 种规格胶合板每张
种规格胶合板每张![]() 元,
元, ![]() 种规格胶合板每张
种规格胶合板每张![]() 元.分别用
元.分别用![]() 表示购买
表示购买![]() 两种不同规格的胶合板的张数.
两种不同规格的胶合板的张数.
(1)用![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(2)根据施工需求, ![]() 两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数.
两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com