
【题目】学校水果店有苹果、梨、香蕉、石榴、橘子、葡萄、西柚等![]() 种水果,西柚数量不多,只够一个人购买,甲乙丙丁戊
种水果,西柚数量不多,只够一个人购买,甲乙丙丁戊![]() 位同学去购买,每人只能选择其中一种,这
位同学去购买,每人只能选择其中一种,这![]() 位同学购买后,恰好买了其中三种水果,则他们购买水果的可能情况有___________种.
位同学购买后,恰好买了其中三种水果,则他们购买水果的可能情况有___________种.
【答案】1170
【解析】
由于西柚水果比较特殊(只够一个人购买),根据![]() 位同学中有没有人买西柚,分成两种情况,即可得出答案.
位同学中有没有人买西柚,分成两种情况,即可得出答案.
(1)假设![]() 位同学中,没有人选择西柚.则
位同学中,没有人选择西柚.则![]() 位同学购买了剩下6种水果里面的3种,
位同学购买了剩下6种水果里面的3种,
则使用隔板法,把![]() 位同学分成3份,共有
位同学分成3份,共有![]() 种分法.
种分法.
再从剩下6种水果里面取3种,共有![]() ,最后把3种水果进行全排列分给5位同学,共有
,最后把3种水果进行全排列分给5位同学,共有![]() 即有:
即有:![]()
![]()
![]() 种情况.
种情况.
(2)假设![]() 位同学中,有一位同学选择西柚.从
位同学中,有一位同学选择西柚.从![]() 位同学中选取一位同学有
位同学中选取一位同学有![]() 种取法,
种取法,
则![]() 位同学购买了剩下6种水果里面的2种,有
位同学购买了剩下6种水果里面的2种,有![]() 种取法.
种取法.
把4位同学分成2份,共有![]() 种分法. 最后把2种水果进行全排列分给4位同学,有
种分法. 最后把2种水果进行全排列分给4位同学,有![]() 种排列.
种排列.
共有:![]()
![]()
![]()
![]() 种情况.
种情况.
故共有:![]()
![]()
![]() +
+![]()
![]()
![]()
![]() =1170种情况.
=1170种情况.
故答案为:1170.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(I)判断曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 的公共点个数;
的公共点个数;
(II)若函数![]() 有且仅有一个零点,求
有且仅有一个零点,求![]() 的值;
的值;
(III)若函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一个最高点为(![]() ),与之相邻的一个对称中心为
),与之相邻的一个对称中心为![]() ,将f(x)的图象向右平移
,将f(x)的图象向右平移![]() 个单位长度得到函数g(x)的图象,则( )
个单位长度得到函数g(x)的图象,则( )
A.g(x)为偶函数
B.g(x)的一个单调递增区间为![]()
C.g(x)为奇函数
D.函数g(x)在![]() 上有两个零点
上有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
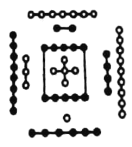
【题目】《易·系辞上》有“河出图,洛出书”之说.河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化,阴阳术数之源.其中河图的排列结构是一、六在后,二、七在前,三、八在左,四、九在右,五、十背中,如图,白圈为阳数,黑点为阴数,若从阴数和阳数中各取一数,则其差的绝对值为1的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为提高产品质量,某企业质量管理部门经常不定期地对产品进行抽查检测,现对某条生产线上随机抽取的100个产品进行相关数据的对比,并对每个产品进行综合评分(满分100分),将每个产品所得的综合评分制成如图所示的频率分布直方图.记综合评分为80分及以上的产品为一等品.
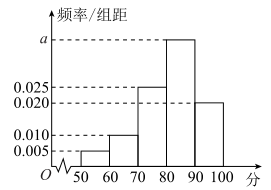
(1)求图中![]() 的值,并求综合评分的中位数;
的值,并求综合评分的中位数;
(2)用样本估计总体,视频率作为概率,在该条生产线中随机抽取3个产品,求所抽取的产品中一等品数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为生产一种精密管件研发了一台生产该精密管件的车床,该精密管件有内外两个口径,监管部门规定“口径误差”的计算方式为:管件内外两个口径实际长分别为![]() ,标准长分别为
,标准长分别为![]() 则“口径误差”为
则“口径误差”为![]() 只要“口径误差”不超过
只要“口径误差”不超过![]() 就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
就认为合格,已知这台车床分昼夜两个独立批次生产.工厂质检部在两个批次生产的产品中分别随机抽取40件作为样本,经检测其中昼批次的40个样本中有4个不合格品,夜批次的40个样本中有10个不合格品.
(Ⅰ)以上述样本的频率作为概率,在昼夜两个批次中分别抽取2件产品,求其中恰有1件不合格产品的概率;
(Ⅱ)若每批次各生产1000件,已知每件产品的成本为5元,每件合格品的利润为10元;若对产品检验,则每件产品的检验费用为2.5元;若有不合格品进入用户手中,则工厂要对用户赔偿,这时生产的每件不合格品工厂要损失25元.以上述样本的频率作为概率,以总利润的期望值为决策依据,分析是否要对每个批次的所有产品作检测?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com