
【题目】设x0为函数f(x)=sinπx的零点,且满足|x0|+f(x0+![]() )<33,则这样的零点有( )
)<33,则这样的零点有( )
A.61个
B.63个
C.65个
D.67个
【答案】C
【解析】∵x0为函数f(x)=sinπx的零点,
∴sinπx0=0,即πx0=kπ,k∈Z,
则x0=k,则f(x0+![]() )=sin(x0+
)=sin(x0+![]() )π=sin(x0+
)π=sin(x0+![]() )π=sin(πx0+
)π=sin(πx0+![]() )=cosπx0 ,
)=cosπx0 ,
若k是偶数,则f(x0+![]() )=1,
)=1,
若k是奇数,则f(x0+![]() )=﹣1,
)=﹣1,
当k是偶数时,则由|x0|+f(x0+![]() )<33得|x0|<﹣f(x0+
)<33得|x0|<﹣f(x0+![]() )+33,
)+33,
即|k|<﹣1+33=32,
则k=﹣30,﹣28,…28,30,共31个,
当k是奇数时,则由|x0|+f(x0+![]() )<33得|x0|<﹣f(x0+
)<33得|x0|<﹣f(x0+![]() )+33,
)+33,
即|k|<1+33=34,
则k=﹣33,﹣31,…31,33,共34个,
故共有31+34=65个,
故选:C.
根据函数零点的定义,先求出x0的值,进行求出f(x0+![]() )的值,然后解不等式即可。
)的值,然后解不等式即可。


科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,已知点A(a,a),B(2,3),C(3,2).
(1)若向量 ![]() ,
, ![]() 的夹角为钝角,求实数a的取值范围;
的夹角为钝角,求实数a的取值范围;
(2)若a=1,点P(x,y)在△ABC三边围成的区域(含边界)上, ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),求m﹣n的最大值.
(m,n∈R),求m﹣n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知递增等比数列{an}满足:a2+a3+a4=28,且a3+2是a2和a4的等差中项,
(1)求数列{an}的通项公式;
(2)若 ![]() ,Sn=b1+b2+…+bn , 求使Sn+n2n+1>62成立的正整数n的最小值.
,Sn=b1+b2+…+bn , 求使Sn+n2n+1>62成立的正整数n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(Ⅰ)若圆![]() 的切线在
的切线在![]() 轴和
轴和![]() 轴上的截距相等,求此切线的方程;
轴上的截距相等,求此切线的方程;
(Ⅱ)从圆![]() 外一点
外一点![]() 向该圆引一条切线,切点为
向该圆引一条切线,切点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,求使
,求使![]() 取得最小值的点
取得最小值的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面图形ABB1A1C1C如图4所示,其中BB1C1C是矩形,BC=2,BB1=4,AB=AC= ![]() ,A1B1=A1C1=
,A1B1=A1C1= ![]() .现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
.现将该平面图形分别沿BC和B1C1折叠,使△ABC与△A1B1C1所在平面都与平面BB1C1C垂直,再分别连接A2A,A2B,A2C,得到如图2所示的空间图形,对此空间图形解答下列问题.
(Ⅰ)证明:AA1⊥BC;
(Ⅱ)求AA1的长;
(Ⅲ)求二面角A﹣BC﹣A1的余弦值.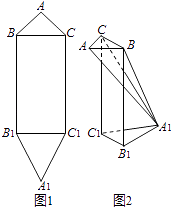
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两点M(﹣3,0),N(3,0),点P为坐标平面内一动点,且![]() ,则动点P(x,y)到两点A(﹣3,0)、B(﹣2,3)的距离之和的最小值为( )
,则动点P(x,y)到两点A(﹣3,0)、B(﹣2,3)的距离之和的最小值为( )
A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O为△ABC的外接圆,D为![]() 的中点,BD交AC于E.
的中点,BD交AC于E.
(Ⅰ)证明:AD2=DEDB;
(Ⅱ)若AD∥BC,DE=2EB,AD=![]() , 求圆O的半径.
, 求圆O的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】半径为1的圆O内切于正方形ABCD,正六边形EFGHPR内接于圆O,当EFGHPR绕圆心O旋转时,![]()
![]() 的取值范围是( )
的取值范围是( )
A.[1﹣![]() , 1+
, 1+![]() ]
]
B.[﹣1-![]() , ﹣1+
, ﹣1+![]() ]
]
C.[![]() ﹣
﹣![]() ,
, ![]() +
+![]() ]
]
D.[-![]() ﹣
﹣![]() , -
, -![]() +
+![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com