
 [lgm+lg(m+2)]×2+
[lgm+lg(m+2)]×2+ [lg(m+2)+lg(m+4)]×2-
[lg(m+2)+lg(m+4)]×2- [lgm+lg(m+4)]×4=2lg(m+2)-lg(m+4)-lgm(m≥1)
[lgm+lg(m+4)]×4=2lg(m+2)-lg(m+4)-lgm(m≥1)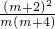 =lg(1+
=lg(1+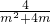 ),(m≥1)
),(m≥1) )这个函数可以看做复合函数
)这个函数可以看做复合函数 最大即可
最大即可 =2lg3-lg5;
=2lg3-lg5;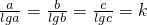 ,k为常数
,k为常数 )这个函数可以看做复合函数,因为S=lgx是增函数,所以要是S最大,只要函数x=1+
)这个函数可以看做复合函数,因为S=lgx是增函数,所以要是S最大,只要函数x=1+ 最大即可,根据函数的单调性可求出最大值;
最大即可,根据函数的单调性可求出最大值;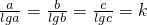 ,k为常数则a、b、c为方程x=klgx的三个根,而曲线y=x与y=klgx至多有两个交点,所以产生矛盾,从而得到结论.
,k为常数则a、b、c为方程x=klgx的三个根,而曲线y=x与y=klgx至多有两个交点,所以产生矛盾,从而得到结论.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
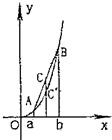 如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,
如图,对于函数f(x)=x3(x>0)上任意两点A(a,a3),B(b,b3)线段AB在弧线段AB的上方,| AC |
| CB |
| a3+b3 |
| 2 |
| a+b |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com