
【题目】如图,在正三棱柱![]() 中,已知
中,已知![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() .求证:
.求证:
(1)直线![]() ∥平面
∥平面![]() ;
;
(2)直线![]() 平面
平面![]() .
.

【答案】(1)详见解析(2)详见解析
【解析】
试题分析:(1)证明线面平行,一般利用线面平行判定定理,即从线线平行出发给予证明,而线线平行的寻找与论证,往往需要利用平几知识,如本题利用平行四边形性质:连结![]() ,可先证得四边形
,可先证得四边形![]() 是平行四边形,进而证得四边形
是平行四边形,进而证得四边形![]() 是平行四边形,即得
是平行四边形,即得![]() ,(2)证明线面垂直,一般利用线面垂直判定与性质定理,经多次转化论证,而在寻找线线垂直时,不仅可利用线面垂直转化,如由
,(2)证明线面垂直,一般利用线面垂直判定与性质定理,经多次转化论证,而在寻找线线垂直时,不仅可利用线面垂直转化,如由![]() 平面
平面![]() ,得
,得![]() ,而且需注意利用平几中垂直条件,如本题中利用正三角形性质得
,而且需注意利用平几中垂直条件,如本题中利用正三角形性质得![]()
试题解析:
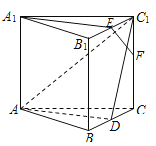
(1)连结![]() ,因为
,因为![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
所以![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,…………………2分
是平行四边形,…………………2分
所以![]() 且
且![]() ,又
,又![]() 且
且![]() ,
,
所以![]() 且
且![]() ,
,
所以四边形![]() 是平行四边形,…………………4分
是平行四边形,…………………4分
所以![]() ,又因为
,又因为![]() ,
,![]() ,
,
所以直线![]() 平面
平面![]() .…………………………………………………7分
.…………………………………………………7分
(2)在正三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() 是正三角形,且
是正三角形,且![]() 为
为![]() 的中点,所以
的中点,所以![]() ,……………9分
,……………9分
又![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,……………………………………11分
,……………………………………11分
又![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以直线平面
![]() .…………………………………………………14分
.…………………………………………………14分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
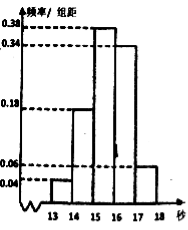
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为![]() ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别![]() ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.
(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,设
,设![]() 为
为![]() 的前
的前![]() 项和.
项和.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)求![]() ;
;
(3)是否存在正整数![]() ,
,![]() ,
,![]()
![]() ,使
,使![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() ,
,![]() ,
,![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的焦点
的焦点![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的周长为短轴长的
的周长为短轴长的![]() 倍.
倍.
(1)求![]() 的离心率;
的离心率;
(2)设![]() 的斜率为
的斜率为![]() ,在
,在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标; 若不存在,说明理由.
的坐标; 若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程![]() ,变量
,变量![]() 增加一个单位时,
增加一个单位时,![]() 平均增加5个单位;③线性回归方程
平均增加5个单位;③线性回归方程![]() 必过
必过![]() ;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
;④在吸烟与患肺病这两个分类变量的计算中,从独立性检验知,有99%的把握认为吸烟与患肺病有关系时,我们说某人吸烟,那么他有99%的可能患肺病;其中错误的个数是( )
A.0 B.1 C. 2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com