
【题目】已知函数![]() .
.
(1)设![]() ,当
,当![]() 时,求函数
时,求函数![]() 的定义域,判断并证明函数
的定义域,判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 上单调递减,且最小值为1?若存在,求出
上单调递减,且最小值为1?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:
【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电实行阶梯收费的方法.为此,相关部门随机调查了20户居民六月分的月用电量(单位:kwh)和家庭月收入(单位:方元)月用电量数据如下18,63,72,82,93,98,106,10,18,130,134,139,147,163,180,194,212,237,260,324家庭月收入数据如下0.21,0.24,0.35,0.40,0.52,0.60,0.58,0.65,0.65,0.63,0.68,0.80,0.83,0.93,0.97,0.96,1.1,1.2,1.5,1.8
(1)根据国家发改委的指示精神,该市实行3阶阶梯电价,使7%的用户在第一档,电价为0.56元/kwh,20%的用户在第二档,电价为0.61元/kwh,5%的用户在第三档,电价为0.86元/kwh,试求出居民用电费用Q与用电量x间的函数关系式;
(2)以家庭月收入t为横坐标,电量x为纵坐标作出散点图(如图)求出x关于t的回归直线方程(系数四舍五入保留整数);

(3)小明家庭月收入7000元,按上述关系,估计小明家月支出电费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,对于函数![]() ,称向量
,称向量![]() 为函数
为函数![]() 的伴随向量,同时称函数
的伴随向量,同时称函数![]() 为向量
为向量![]() 的伴随函数.
的伴随函数.
(1)设函数![]() ,试求
,试求![]() 的伴随向量
的伴随向量![]() ;
;
(2)记向量![]() 的伴随函数为
的伴随函数为![]() ,求当
,求当![]() 且
且![]() 时
时![]() 的值;
的值;
(3)由(1)中函数![]() 的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移
的图象(纵坐标不变)横坐标伸长为原来的2倍,再把整个图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,已知
的图象,已知![]() ,
,![]() ,问在
,问在![]() 的图象上是否存在一点P,使得
的图象上是否存在一点P,使得![]() .若存在,求出P点坐标;若不存在,说明理由.
.若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图为某市国庆节7天假期的楼房认购量与成交量的折线图,小明同学根据折线图对这7天的认购量(单位:套)与成交量(单位:套)作出如下判断:①日成交量的中位数是26;②日成交量超过日平均成交量的有2天;③认购量与日期正相关;④10月2日到10月6日认购量的分散程度比成交量的分散程度更大.则上述判断错误的个数为( )
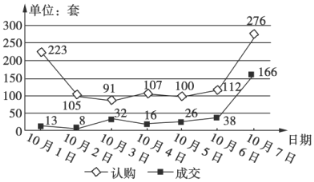
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际象棋比赛中.胜局一得1分,平一局得0.5分,负一局得0分。今有8名选手进行单循环比赛(每两人均赛一局),赛完后、发现各选手的得分均不相同,当按得分由大到小排列好名次后,第四名选手得4.5分,第二名的得分等于最后四名选手得分总和.问前三名选手各得多少分?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”
”
B.“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
C.直线![]() :
:![]() ,
,![]() :
:![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
D.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018河南豫南九校高三下学期第一次联考】设函数![]() .
.
(I)当![]() 时,
时, ![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(II)若![]() 在
在![]() 处的切线为
处的切线为![]() ,且方程
,且方程![]() 恰有两解,求实数
恰有两解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ),曲线
),曲线![]() (
(![]() 为参数,实数
为参数,实数![]() ).在以
).在以![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,射线
轴的正半轴为极轴的极坐标系中,射线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() ;当
;当![]() ,
,![]() .
.
(1)求![]() 和
和![]() 的值.
的值.
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校初中部共120名教师,高中部共180名教师,其性别比例如图所示,已知按分层抽样方法得到的工会代表中,高中部女教师有6人,则工会代表中男教师的总人数为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com