
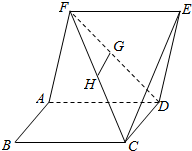
 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.分析 (1)由AF∥DE,得∠CED是异面直线AF与CE所成角,由此能求出异面直线AF与CE所成角的大小.
(2)由G,H是DF,FC的中点,得GH∥CD,由此能证明GH∥平面CDE.
解答 解:(1)∵正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,
∴CD⊥DE,CD=DE=1,AF∥DE,∴∠CED是异面直线AF与CE所成角,
∵CD⊥DE,CD=DE=1,
∴∠CED=45°,
∴异面直线AF与CE所成角为45°.
证明:(2)∵G,H是DF,FC的中点,
∴GH∥CD,
∵GH?平面CDE,CD?平面CDE,
∴GH∥平面CDE.
点评 本题考查异面直线所成角的大小的求法,考查线面平行的证明,是基础题,解题时要认真审题,注意空间思维能力的培养.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$ | ||
| C. | y=21+x+21-x | D. | y=x2+$\frac{1}{{x}^{2}+1}$+3,x≠0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | (-∞,-1)∪(3,+∞) | C. | (-3,1) | D. | (-∞,-3)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com