
【题目】已知数列{an}满足log3an+1=log3an+1(n∈N*),且a2+a4+a6=9,则log ![]() (a5+a7+a9)的值是( )
(a5+a7+a9)的值是( )
A.﹣ ![]()
B.﹣5
C.5
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过点
经过点![]() 、
、![]() ,并且直线
,并且直线![]() :
: ![]() 平分圆
平分圆![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若过点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() 与圆
与圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(ⅰ)求实数![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点是
的两个焦点是![]() 和
和![]() ,并且经过点
,并且经过点![]() ,抛物线
,抛物线![]() 的顶点在坐标原点,焦点恰好是椭圆
的顶点在坐标原点,焦点恰好是椭圆![]() 的右顶点.
的右顶点.
(Ⅰ)求椭圆![]() 和抛物线
和抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)已知点![]() 为抛物线
为抛物线![]() 内一个定点,过
内一个定点,过![]() 作斜率分别为
作斜率分别为![]() 的两条直线交抛物线
的两条直线交抛物线![]() 于点
于点![]() ,且
,且![]() 分别是
分别是![]() 的中点,若
的中点,若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 的动点,过
的动点,过![]() 的平面截该正方体所得的截面记为
的平面截该正方体所得的截面记为![]() ,则下列命题正确的序号是_________.
,则下列命题正确的序号是_________.
①当![]() 时,
时, ![]() 的面积为
的面积为![]() ;
;
②当![]() 时,
时, ![]() 为六边形;
为六边形;
③当![]() 时,
时, ![]() 与
与![]() 的交点
的交点![]() 满足
满足![]() ;
;
④当![]() 时,
时, ![]() 为等腰梯形;
为等腰梯形;
⑤当![]() 时,
时, ![]() 为四边形.
为四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(m,cos2x),
=(m,cos2x), ![]() =(sin2x,n),设函数f(x)=
=(sin2x,n),设函数f(x)= ![]()
![]() ,且y=f(x)的图象过点(
,且y=f(x)的图象过点( ![]() ,
, ![]() )和点(
)和点( ![]() ,﹣2). (Ⅰ)求m,n的值;
,﹣2). (Ⅰ)求m,n的值;
(Ⅱ)将y=f(x)的图象向左平移φ(0<φ<π)个单位后得到函数y=g(x)的图象.若y=g(x)的图象上各最高点到点(0,3)的距离的最小值为1,求y=g(x)的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟) |
|
|
|
|
|
次数 | 8 | 14 | 8 | 8 | 2 |
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为![]() 分钟.
分钟.
(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设![]() 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列{an},定义 ![]() 为{an}的“优值”,现在已知某数列{an}的“优值”
为{an}的“优值”,现在已知某数列{an}的“优值” ![]() ,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
,记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n∈N+恒成立,则实数k的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的部分图象如图所示.
的部分图象如图所示. 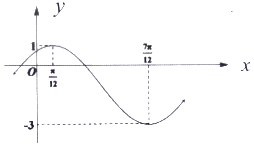
(1)求f(x)的解析式;
(2)求f(x)的单调递增区间和对称中心坐标;
(3)将f(x)的图象向左平移 ![]() 个单位,再讲横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在
个单位,再讲横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数g(x)的图象,求函数y=g(x)在 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]()
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() 的斜率
的斜率![]() 满足
满足![]() 求
求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com