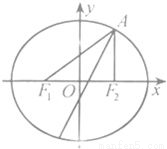
分析:(Ⅰ)设椭圆方程为
+
=1,把点A(2,3)代入椭圆方程,把离心率e=
用a,c表示,再根据b
2=a
2-c
2,求出a
2,b
2,得椭圆方程;
(Ⅱ)可以设直线l上任一点坐标为(x,y),根据角平分线上的点到角两边距离相等得
=|x-2|.
解答:解:(Ⅰ)设椭圆E的方程为
+
=1
由e=
,得
=,b
2=a
2-c
2=3c
2,∴
+=1将A(2,3)代入,有
+=1,解得:c=2,
∴椭圆E的方程为
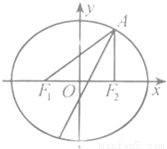
+=1(Ⅱ)由(Ⅰ)知F
1(-2,0),F
2(2,0),所以直线AF
1的方程为y=
(x+2),
即3x-4y+6=0,直线AF
2的方程为x=2,由椭圆E的图形知,∠F
1AF
2的角平分线所在直线的斜率为正数
设P(x,y)为∠F
1AF
2的角平分线所在直线上任一点,则有
=|x-2|
若3x-4y+6=-5x+10,得x+2y-8=0,其斜率为负,不合题意,舍去.
于是3x-4y+6=10-5x,即x+2y-8=0.
所以,∠F
1AF
2的角平分线所在直线的方程为x+2y-8=0
点评:对于椭圆解答题,一般都是设椭圆方程为
+
=1,根据题目满足的条件求出a
2,b
2,得椭圆方程,这一问通常比较简单;(2)对于角平分线问题,利用角平分线的几何意义,即角平分线上的点到角两边距离相等得方程.

 椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=
椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=

 已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=
已知椭圆E经过点A(2,3),对称轴为坐标轴,焦点F1,F2在x轴上,离心率e=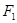 、
、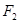 在x轴上,离心率
在x轴上,离心率
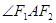 的角平分线所在直线
的角平分线所在直线 的方程.
的方程.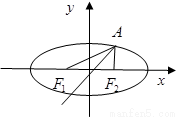
 .
.
 .
.