
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE. 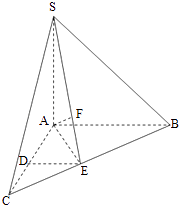
(1)求证:AF⊥平面SBC;
(2)在线段上DE上是否存在点G,使二面角G﹣AF﹣E的大小为30°?若存在,求出DG的长;若不存在,请说明理由.
【答案】
(1)证明:由AC=AB=SA=2,AC⊥AB,E是BC的中点,得 ![]() .
.
因为SA⊥底面ABC,所以SA⊥AE.
在Rt△SAE中, ![]() ,所以
,所以 ![]() .
.
因此AE2=EFSE,又因为∠AEF=∠AES,
所以△EFA∽△EAS,
则∠AFE=∠SAE=90°,即AF⊥SE.
因为SA⊥底面ABC,所以SA⊥BC,又BC⊥AE,
所以BC⊥底面SAE,则BC⊥AF.
又SE∩BC=E,所以AF⊥平面SBC
(2)解:结论:在线段上DE上存在点G使二面角G﹣AF﹣E的大小为30°,此时DG= ![]() .
.
理由如下:
假设满足条件的点G存在,并设DG=t.
过点G作GM⊥AE交AE于点M,
又由SA⊥GM,AE∩SA=A,得GM⊥平面SAE.
作MN⊥AF交AF于点N,连结NG,则AF⊥NG.
于是∠GNM为二面角G﹣AF﹣E的平面角,
即∠GNM=30°,由此可得 ![]() .
.
由MN∥EF,得 ![]() ,
,
于是有 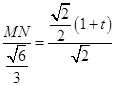 ,
, ![]() .
.
在Rt△GMN中,MG=MNtan30°,
即 ![]() ,解得
,解得 ![]() .
.
于是满足条件的点G存在,且 ![]() .
.
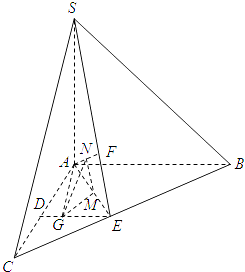
【解析】(1)通过证明AF与平面SBC内的两条相交直线垂直即可;(2)抓住两点找到问题的求解方向:一是点G的预设位置,二是二面角G﹣AF﹣E的位置,计算即可.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ![]() ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ![]() ,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为x,求x≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() 当x∈[﹣
当x∈[﹣ ![]() ,
, ![]() ]时,恒有f(x+a)<f(x),则实数a的取值范围是( )
]时,恒有f(x+a)<f(x),则实数a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.(﹣1, ![]() )
)
C.( ![]() ,0)
,0)
D.( ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足an= ![]() ,若从{an}中提取一个公比为q的等比数列{a
,若从{an}中提取一个公比为q的等比数列{a ![]() },其中k1=1且k1<k2<…<kn , kn∈N*,则满足条件的最小q的值为( )
},其中k1=1且k1<k2<…<kn , kn∈N*,则满足条件的最小q的值为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aex﹣xlnx,其中a∈R,e是自然对数的底数.
(Ⅰ)若f(x)是(0,+∞)上的增函数,求a的取值范围;
(Ⅱ)若 ![]() ,证明:f(x)>0.
,证明:f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医疗科研项目对5只实验小白鼠体内的A、B两项指标数据进行收集和分析,得到的数据如下表:
指标 | 1号小白鼠 | 2号小白鼠 | 3号小白鼠 | 4号小白鼠 | 5号小白鼠 |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
(1)若通过数据分析,得知A项指标数据与B项指标数据具有线性相关关系,试根据上表,求B项指标数据y关于A项指标数据x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)现要从这5只小白鼠中随机抽取3只,求其中至少有一只B项指标数据高于3的概率. 参考公式: ![]() =
= 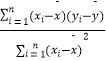 =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,曲线y=f(x)在点(e2 , f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).
,曲线y=f(x)在点(e2 , f(e2))处的切线与直线2x+y=0垂直(其中e为自然对数的底数).
(1)求f(x)的解析式及单调递减区间;
(2)若存在x0∈[e,+∞),使函数g(x)=aelnx+ ![]() lnxf(x)≤a成立,求实数a的取值范围.
lnxf(x)≤a成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com