
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
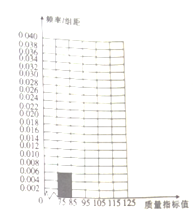
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |
科目:高中数学 来源: 题型:
【题目】(1)7名学生站成一排,甲、乙只能站在两端的排法有多少种?(结果用数值表示)
(2)7名学生站成一排,甲、乙不能站在排头和排尾的排法有多少种?
(3)7名学生站成一排,甲、乙和丙3名学生必须相邻的排法有多少种?
(4)7名学生站成一排,甲、乙两名学生必须相邻,而且丙不能站在排头与排尾的排法有多少种?
(5)7名学生站成一排,甲、乙和丙3名学生都不能相邻的排法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆方程为![]() ,其右焦点
,其右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 且垂直于抛物线对称轴的直线与椭圆交于
且垂直于抛物线对称轴的直线与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.
两点.![]()
(1)求椭圆的方程;
(2)若直线l与(1)中椭圆相交于![]() ,
,![]() 两点, 直线
两点, 直线![]() ,
, ![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() (其中
(其中![]() ),且
),且![]() ,
,![]() ,
,![]() 成等比数列;设
成等比数列;设![]() 的面积为
的面积为![]() , 以
, 以![]() 、
、![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
, ![]() , 求
, 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,试问在曲线
,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() (
(![]() 为坐标原点)为平行四边形?若存在,求出直线
为坐标原点)为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某居民区有一个银行网点(以下简称“网点”),网点开设了若干个服务窗口,每个窗口可以办理的业务都相同,每工作日开始办理业务的时间是8点30分,8点30分之前为等待时段.假设每位储户在等待时段到网点等待办理业务的概率都相等,且每位储户是否在该时段到网点相互独立.根据历史数据,统计了各工作日在等待时段到网点等待办理业务的储户人数,得到如图所示的频率分布直方图:
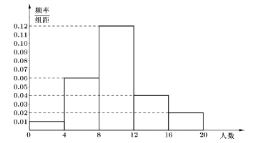
(1)估计每工作日等待时段到网点等待办理业务的储户人数的平均值;
(2)假设网点共有1000名储户,将频率视作概率,若不考虑新增储户的情况,解决以下问题:
①试求每位储户在等待时段到网点等待办理业务的概率;
②储户都是按照进入网点的先后顺序,在等候人数最少的服务窗口排队办理业务.记“每工作日上午8点30分时网点每个服务窗口的排队人数(包括正在办理业务的储户)都不超过3”为事件![]() ,要使事件
,要使事件![]() 的概率不小于0.75,则网点至少需开设多少个服务窗口?
的概率不小于0.75,则网点至少需开设多少个服务窗口?
参考数据:![]() ;
;![]() ;
;
![]() ;
;![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com