
【题目】对于数列{an}、{bn},Sn为数列{an}的前n项和,且Sn+1﹣(n+1)=Sn+an+n,a1=b1=1,bn+1=3bn+2,n∈N* .
(1)求数列{an}、{bn}的通项公式;
(2)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
【答案】
(1)解:由Sn+1﹣(n+1)=Sn+an+n,
∴Sn+1﹣Sn=an+2n+1,
∴an+1﹣an=2n+1,
∴a2﹣a1=2×1+1,
a3﹣a2=2×2+1,
a4﹣a3=2×3+1,
…
an﹣an﹣1=2(n﹣1)+1,
以上各式相加可得:an﹣a1=2×(1+2+3+…+n﹣1)+(n﹣1),
∴an=2× ![]() +(n﹣1)+1=n2,
+(n﹣1)+1=n2,
∴an=n2,
∵bn+1=3bn+2,即bn+1+1=3(bn+1),
b1+1=2,
∴数列{bn+1}是以2为首项,以3为公比的等比数列,
bn+1=2×3n﹣1,
∴bn=2×3n﹣1﹣1;
(2)解:由(1)可知:cn= ![]() =
= ![]() =
= ![]() ,
,
∴Tn=c1+c2+…+cn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,
,
![]() Tn=
Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,
,
∴ ![]() Tn=2+
Tn=2+ ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() ,
,
=2+ ![]() ﹣
﹣ ![]() ,
,
= ![]() ﹣
﹣ ![]() ,
,
∴Tn= ![]() ﹣
﹣ ![]() ,
,
数列{cn}的前n项和Tn,Tn= ![]() ﹣
﹣ ![]()
【解析】(1)由Sn+1﹣Sn=an+2n+1,则an+1﹣an=2n+1,利用“累加法”即可求得an=n2 , 由bn+1+1=3(bn+1),可知数列{bn+1}是以2为首项,以3为公比的等比数列,即可求得{bn}的通项公式;(2)由(1)可知:cn= ![]() =
= ![]() =
= ![]() ,利用“错位相减法”即可求得数列{cn}的前n项和Tn .
,利用“错位相减法”即可求得数列{cn}的前n项和Tn .
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系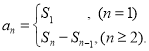 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】为了了解小学生的体能情况,抽取某校一个年级的部分学生进行一分钟跳绳次数的测试,将数据整理后,画出频率分布直方图如图所示.已知图中从左到右前三个小组的频率分别为0.1,0.3,0.4,且第一小组的频数为5.
(1)求第四小组的频率;
(2)求参加这次测试的学生的人数;
(3)若一分钟跳绳次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在创建全国旅游城市的活动中,对一块以O为圆心,R(R为常数,单位:米)为半径的半圆形荒地进行治理改造,其中弓形BCD区域(阴影部分)种植草坪,△OBD区域用于儿童乐园出租,其余区域用于种植观赏植物.已知种植草坪和观赏植物的成本分别是每平方米5元和55元,儿童乐园出租的利润是每平方米95元.
(1)设∠BOD=θ(单位:弧度),用θ表示弓形BCD的面积S弓=f(θ).
(2)如果该市规划办邀请你规划这块土地,如何设计∠BOD的大小才能使总利润最大?并求出最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且S4=4S2 , a2+a4=10.
(1)求数列{an}通项公式;
(2)若数列{bn}满足 ![]() +
+ ![]() +…+
+…+ ![]() =1﹣
=1﹣ ![]() ,n∈N* , 求数列{bn}的前n项和Tn .
,n∈N* , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a,b,c分别为内角A,B,C所对边的边长,且满足![]() a-2bsin A=0.
a-2bsin A=0.
(1)求角B的大小;
(2)若a+c=5,且a>c,b=![]() ,求
,求![]() ·
·![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com