
【题目】已知函数f(x)=6cos2![]() +
+![]() sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.

(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=![]() ,且x0∈(-
,且x0∈(-![]() ,
,![]() ),求f(x0+1)的值.
),求f(x0+1)的值.
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)为奇函数,当x≥0时,f(x)= ![]() .g(x)=
.g(x)= ![]() ,
,
(1)求当x<0时,函数f(x)的解析式,并在给定直角坐标系内画出f(x)在区间[﹣5,5]上的图象;(不用列表描点) 
(2)根据已知条件直接写出g(x)的解析式,并说明g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[﹣2,t](t>﹣2)上的函数f(x)=(x2﹣3x+3)ex(其中e为自然对数的底).
(1)当t>1时,求函数y=f(x)的单调区间;
(2)设m=f(﹣2),n=f(t),求证:m<n;
(3)设g(x)=f(x)+(x﹣2)ex , 当x>1时,试判断方程g(x)=x的根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代算书《孙子算经》中有一著名的问题“物不知数”如图1,原题为:今有物,不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?后来,南宋数学家秦九韶在其著作《数学九章》中对此类问题的解法做了系统的论述,并称之为“大衍求一术”,如图2程序框图的算法思路源于“大衍求一术”执行该程序框图,若输入的a,b分别为20,17,则输出的c=( )
A.1
B.6
C.7
D.11
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】化简
(1)![]()
(2)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)切化弦可得三角函数式的值为-1
(2)结合三角函数的性质可得三角函数式的值为![]()
试题解析:
(1)tan70°cos10°( ![]() tan20°﹣1)
tan20°﹣1)
=cot20°cos10°( ![]() ﹣1)
﹣1)
=cot20°cos10°(![]() )
)
=![]() ×cos10°×(
×cos10°×(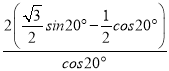 )
)
=![]() ×cos10°×(
×cos10°×(![]() )
)
=![]() ×(﹣
×(﹣![]() )
)
=﹣1
(2)∵(1+tan1°)(1+tan44°)=1+(tan1°+tan44°)+tan1°tan44°
=1+tan(1°+44°)[1﹣tan1°tan44°]+tan1°tan44°=2.
同理可得(1+tan2°)(1+tan43°)
=(1+tan3°)(1+tan42°)
=(1+tan4°)(1+tan41°)=…=2,
故![]() =
=![]()
点睛:三角函数式的化简要遵循“三看”原则:一看角,这是重要一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式 ;二看函数名称,看函数名称之间的差异,从而确定使用的公式,常见的有切化弦;三看结构特征,分析结构特征,可以帮助我们找到变形的方向,如遇到分式要通分等.
【题型】解答题
【结束】
18
【题目】平面内给定三个向量![]()
(1)求![]()
(2)求满足![]() 的实数
的实数![]() .
.
(3)若![]() ,求实数
,求实数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子里装有7个球,其中有红球4个,编号分别为1,2,3,4;白球3个,编号分别为2,3,4.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中,含有编号为3的球的概率;
(Ⅱ)在取出的4个球中,红球编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣ ![]() 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ ![]() <a<﹣
<a<﹣ ![]() 时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 上有最大值4和最小值1.设
上有最大值4和最小值1.设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com