
【题目】某个部件由三个元件按图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作(其中元件1,2,3正常工作的概率都为 ![]() ),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )
),设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( ) 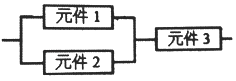
A.![]()
B.![]()
C.![]()
D.![]()
科目:高中数学 来源: 题型:
【题目】若函数f(x)=2sin( ![]() )(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(
)(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则( ![]() +
+ ![]() )
) ![]() =( )
=( )
A.﹣32
B.﹣16
C.16
D.32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项都是正数,且对任意n∈N* , 都有(an﹣1)(an+3)=4Sn , 其中Sn为数列{an}的前n项和.
(1)求证数列{an}是等差数列;
(2)若数列{ ![]() }的前n项和为Tn , 求Tn .
}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.如果命题“¬p”与命题“p∨q”都是真命题,那么命题q一定是真命题
B.命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”
C.若命题p:?x0∈R,x02+2x0﹣3<0,则?p:?x∈R,x2+2x﹣3≥0
D.“sinθ= ![]() ”是“θ=30°”的充分不必要条件
”是“θ=30°”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是棱
是棱![]() 上一点.
上一点.

(I)求证: ![]() .
.
(II)若![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() .
.
(III)若二面角![]() 的大小为
的大小为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com