
【题目】设a,b∈R,若x≥0时恒有0≤x4﹣x3+ax+b≤(x2﹣1)2,则ab等于 _________ .
【答案】﹣1
【解析】
验证发现,
当x=1时,将1代入不等式有0≤a+b≤0,所以a+b=0,
当x=0时,可得0≤b≤1,结合a+b=0可得﹣1≤a≤0
令f(x)=x4﹣x3+ax+b,即f(1)=a+b=0
又f′(x)=4x3﹣3x2+a,f′′(x)=12x2﹣6x,
令f′′(x)>0,可得x>![]() ,则f′(x)=4x3﹣3x2+a在[0,
,则f′(x)=4x3﹣3x2+a在[0,![]() ]上减,在[
]上减,在[![]() ,+∞)上增
,+∞)上增
又﹣1≤a≤0,所以f′(0)=a<0,f′(1)=1+a≥0
又x≥0时恒有0≤x4﹣x3+ax+b,结合f(1)=a+b=0知,1必为函数f(x)=x4﹣x3+ax+b的极小值点,也是最小值点
故有f′(1)=1+a=0,由此得a=﹣1,b=1
故ab=﹣1
故答案为﹣1


科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,底面ABCD是等腰梯形,
中,底面ABCD是等腰梯形,![]() ,
,![]() ,
,![]() ,顶点
,顶点![]() 在底面ABCD内的射影恰为点C.
在底面ABCD内的射影恰为点C.

(1)求证:BC⊥平面ACD1;
(2)若直线DD1与底面ABCD所成的角为![]() ,求平面
,求平面![]() 与平面ABCD所成锐二面角的余弦值.
与平面ABCD所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为
的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为![]() ,且椭圆的离心率为
,且椭圆的离心率为![]() .
.
(1)求椭圆C的标准方程:
(2)设点P为椭圆C的下顶点,直线PA,PB与y=2分别交于点M,N,当|MN|最小时,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,O为BE中点,F为BC中点.将
,O为BE中点,F为BC中点.将![]() 沿BE折起到
沿BE折起到![]() 的位置,如图2.
的位置,如图2.

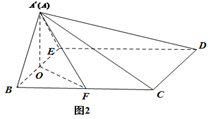
(1)证明:![]() 平面
平面![]() ;
;
(2)若平面![]() 平面BCDE,求点F到平面
平面BCDE,求点F到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)若![]() ,求直线
,求直线![]() 的普通方程及曲线
的普通方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 为定点,点
为定点,点![]() 为
为![]() 的中点,动点
的中点,动点![]() 满足
满足![]() ,且
,且![]() ,设点
,设点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 的直线交曲线
的直线交曲线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 为曲线
为曲线![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点.问
两点.问![]() 是否为定值?若是,求
是否为定值?若是,求![]() 的值;若不是,请说明理由.
的值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com