
【题目】已知![]() 是公差不为零的等差数列,
是公差不为零的等差数列, ![]() 是等比数列,且
是等比数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若满足不等式![]() 成立的
成立的![]() 恰有
恰有![]() 个,求正整数
个,求正整数![]() 的值.
的值.
【答案】(1) ![]() ,
,![]() .(2)
.(2) ![]() .(3)
.(3) ![]() .
.
【解析】分析:(1) 根据![]() ,
,![]() ,
,![]() 列出关于首项
列出关于首项![]() 、
、![]() ,公差
,公差![]() 与公比
与公比![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 、
、![]() ,公差
,公差![]() 与公比
与公比![]() 的值,从而可得数列
的值,从而可得数列![]() ,
,![]() 的通项公式;(2)由(1)可得
的通项公式;(2)由(1)可得![]() ,利用错位相减法求和即可的结果;(3) 不等式
,利用错位相减法求和即可的结果;(3) 不等式![]() 可化为
可化为![]() ,先判断
,先判断![]() 的增减性,可得则
的增减性,可得则![]() 时,
时, ![]() 中最大的三项值为
中最大的三项值为![]() ,由
,由![]() 时满足
时满足![]() 的
的![]() 共有两个,可得
共有两个,可得![]() ,由
,由![]() 解得
解得![]() ,则正整数
,则正整数![]() .
.
详解: (1)设![]() 的公差为
的公差为![]() ,
, ![]() 的公比为
的公比为![]() ,
,
![]() ,
,![]() ;
;![]() ,
,![]() ;
;
由![]() ,
,![]() 可得
可得![]() ,
,![]() ,
,
由![]() 可得
可得![]() ,
,
则![]() ,
,![]() ,
,
则![]() ,
,![]() ;
;
(2) ![]() ,
,
![]()
![]()
![]()
![]()
作差可得![]()
![]()
![]() ,
,
则![]()
![]() ;
;
(3) 不等式![]() 可化为
可化为![]() ,
,
即![]()
![]() ,即
,即![]() ,
,
![]() ,
,![]() 时一定成立,
时一定成立,
则![]() 时,满足
时,满足![]() 的
的![]() 共有两个,此时
共有两个,此时![]() ,
,![]() ,
,
即满足![]() 的
的![]() 共有两个,
共有两个,
令![]() ,
,![]() ,
,
![]()
![]() ,
,
则![]() 时,
时, ![]()
![]() 时,
时, ![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() 时,
时, ![]() 中最大的三项值为
中最大的三项值为![]() ,
,
由![]() 时满足
时满足![]() 的
的![]() 共有两个,可得
共有两个,可得![]() ,
,
由![]() 解得
解得![]() ,则正整数
,则正整数![]() .
.


科目:高中数学 来源: 题型:
【题目】某科研小组有20个不同的科研项目,每年至少完成一项。有下列两种完成所有科研项目的计划:
A计划:第一年完成5项,从第一年开始,每年完成的项目不得少于次年,直到全部完成为止;
B计划:第一年完成项数不限,从第一年开始,每年完成的项目不得少于次年,恰好5年完成所有项目。
那么,按照A计划和B计划所安排的科研项目不同完成顺序的方案数量
A. 按照A计划完成的方案数量多
B. 按照B计划完成的方案数量多
C. 按照两个计划完成的方案数量一样多
D. 无法判断哪一种计划的方案数量多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 轴的垂线段
轴的垂线段![]() ,
, ![]() 为垂足.当点
为垂足.当点![]() 在圆
在圆![]() 上运动时,线段
上运动时,线段![]() 中点
中点![]() 的轨迹为曲线
的轨迹为曲线![]() (包括点
(包括点![]() 和点
和点![]() ),
),![]() 为坐标原点.
为坐标原点.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)直线![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与圆
与圆![]() 相交于
相交于![]() 两点,当
两点,当![]() 的面积最大时,试求直线
的面积最大时,试求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() ;③若
;③若![]() ,则
,则![]() ;④若
;④若![]() ,
, ![]() 且
且![]() ,则
,则![]() 的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
的最小值为9;其中正确命题的序号是______(将你认为正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]()
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上有且只有一个极值点,求实数
在定义域上有且只有一个极值点,求实数![]() 的取值范围;
的取值范围;
(3)若对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生研究学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设![]() 表示学生注意力指标.
表示学生注意力指标.
该小组发现![]() 随时间
随时间![]() (分钟)的变化规律(
(分钟)的变化规律(![]() 越大,表明学生的注意力越集中)如下:
越大,表明学生的注意力越集中)如下: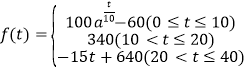 (
(![]() 且
且![]() ).
).
若上课后第![]() 分钟时的注意力指标为
分钟时的注意力指标为![]() ,回答下列问题:
,回答下列问题:
(![]() )求
)求![]() 的值.
的值.
(![]() )上课后第
)上课后第![]() 分钟和下课前
分钟和下课前![]() 分钟比较,哪个时间注意力更集中?并请说明理由.
分钟比较,哪个时间注意力更集中?并请说明理由.
(![]() )在一节课中,学生的注意力指标至少达到
)在一节课中,学生的注意力指标至少达到![]() 的时间能保持多长?
的时间能保持多长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的x轴的正半轴重合,且两个坐标系的单位长度相同.已知直线l的参数方程为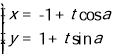 (t为参数),曲线C的极坐标方程为
(t为参数),曲线C的极坐标方程为![]() .
.
(Ⅰ)若直线l的斜率为-1,求直线l与曲线C交点的极坐标;
(Ⅱ)若直线l与曲线C相交弦长为![]() ,求直线l的参数方程(标准形式).
,求直线l的参数方程(标准形式).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com