
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数(万台) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
该产品的年利润(百万元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修台数(台) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分计算结果:
| ||||||||
注:年返修率=![]()
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的线性回归方程(精确到0.01).
(万台)的线性回归方程(精确到0.01).
附:线性回归方程![]() 中,
中,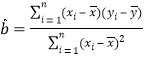
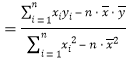 ,
,![]() .
.
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过两点
经过两点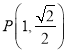 ,
,![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过椭圆的右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,且直线
两点,且直线![]() 与以线段
与以线段![]() 为直径的圆交于另一点
为直径的圆交于另一点![]() (异于点
(异于点![]() ),若
),若![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】百年双中的校训是“仁”、“智”、“雅”、“和”.在2019年5月18日的高三趣味运动会中有这样的一个小游戏.袋子中有大小、形状完全相同的四个小球,分别写有“仁”、“智”、“雅”、“和”四个字,有放回地从中任意摸出一个小球,直到“仁”、“智”两个字都摸到就停止摸球.小明同学用随机模拟的方法恰好在第三次停止摸球的概率.利用电脑随机产生1到4之间(含1和4)取整数值的随机数,分别用1,2,3,4代表“仁”、“智”、“雅”、“和”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下20组随机数:
141 432 341 342 234 142 243 331 112 322
342 241 244 431 233 214 344 142 134 412
由此可以估计,恰好第三次就停止摸球的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月郑州市被国务院确定为全国46个生活垃圾分类处理试点城市之一,此后由郑州市城市管理局起草公开征求意见,经专家论证,多次组织修改完善,数易其稿,最终形成《郑州市城市生活垃圾分类管理办法》(以下简称《办法》).《办法》已于2019年9月26日被郑州市人民政府第35次常务会议审议通过,并于2019年12月1日开始施行.《办法》中将郑州市生活垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他垃圾4类.为了获悉高中学生对垃圾分类的了解情况,某中学设计了一份调查问卷,500名学生参加测试,从中随机抽取了100名学生问卷,记录他们的分数,将数据分成7组:![]() ,
,![]() ,…,
,…,![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
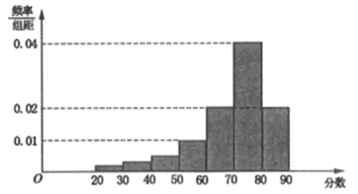
(1)从总体的500名学生中随机抽取一人,估计其分数不低于60的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的学生人数,
内的学生人数,
(3)学校环保志愿者协会决定组织同学们利用课余时间分批参加“垃圾分类,我在实践”活动,以增强学生的环保意识.首次活动从样本中问卷成绩低于40分的学生中随机抽取2人参加,已知样本中分数小于40的5名学生中,男生3人,女生2人,求抽取的2人中男女同学各1人的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
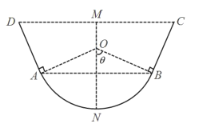
【题目】某农场计划设计建造一条2000米长的水渠,其横断面如图所示.其中,底部是半径为1米的圆弧![]() ,上部是有一定倾角的线段
,上部是有一定倾角的线段![]() 与
与![]() ,渠深
,渠深![]() 为
为![]() 米,且圆弧
米,且圆弧![]() 的圆心为O在
的圆心为O在![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() .据测算,水渠底部曲面每平方米的造价为
.据测算,水渠底部曲面每平方米的造价为![]() 百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设
百元,上部矩形壁面每平方米的造价为1百元,其他费用忽略不计.设![]() ,
,![]() .
.
(1)试用![]() 表示水渠建造的总费用
表示水渠建造的总费用![]() (单位:百元);
(单位:百元);
(2)试确定![]() 的值,使得建造总费用最低.
的值,使得建造总费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com