
【题目】如图所示,正三角形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
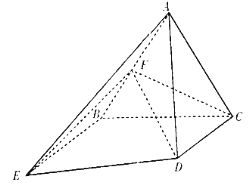
(1)求证: ![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为30°,求三棱锥
所成的角为30°,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)先根据面面垂直性质定理转化为线面垂直![]() 平面
平面![]() ,,再利用线面垂直性质定理得线线垂直
,,再利用线面垂直性质定理得线线垂直![]() ,由正三角形性质得
,由正三角形性质得![]() ,最后根据线面垂直判定定理得结论,(2)先根据线面垂直
,最后根据线面垂直判定定理得结论,(2)先根据线面垂直![]() 平面
平面![]() 确定直线
确定直线![]() 与平面
与平面![]() 所成的角的平面角为
所成的角的平面角为![]() ,求出点
,求出点![]() 到平面
到平面![]() 的距离,根据
的距离,根据![]() 为
为![]() 的中点,可得点
的中点,可得点![]() 到平面
到平面![]() 的距离为点
的距离为点![]() 到平面
到平面![]() 的距离一半,利用锥体体积公式可得
的距离一半,利用锥体体积公式可得![]() ,再根据等体积法可得
,再根据等体积法可得![]() .
.
试题解析:(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 为正三角形,
为正三角形, ![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
易知![]() 平面
平面![]() ,∴
,∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
∵![]() 中,
中, ![]() ,∴
,∴![]() ,
,
∵![]() 为正三角形,
为正三角形, ![]() 为
为![]() 的中点,
的中点,
∴![]() 且
且![]() ,
,
∵平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 为
为![]() 的中点,∴点
的中点,∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】在公差为d的等差数列{an}中,已知a1=10,5a1a3=(2a2+2)2 .
(1)求d和an的值;
(2)若d<0,求|a1|+|a2|+|a3|+…+|a2021|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin
sin ![]() cos
cos ![]() +sin2
+sin2 ![]() (ω>0,0<φ<
(ω>0,0<φ< ![]() ).其图象的两个相邻对称中心的距离为
).其图象的两个相邻对称中心的距离为 ![]() ,且过点(
,且过点( ![]() ,1).
,1).
(1)函数f(x)的解析式;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c.已知 ![]() =
= ![]() .且f(A)=
.且f(A)= ![]() ,求角C的大小.
,求角C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了解学生在课外读物方面的支出情况,抽取了n名同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在[30,50)(单位:元)的同学有67人,其频率分布直方图如图所示,则n的值为( )
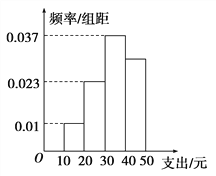
A. 100 B. 120 C. 130 D. 390
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)在区间[1,3]上任取两整数a、b,求二次方程x2+2ax+b2=0有实数根的概率.
(2)在区间[1,3]上任取两实数a、b,求二次方程x2+2ax+b2=0有实数根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com