
(1)用1、2、3、4、5、6、7可组成多少个无重复数字的四位数且四位数为偶数;
(2)用0、1、2、3、4、5可组成多少无重复数字的且可被5整除的五位数. (用数字作答)
(1)360(2)216
解析试题分析:解:(1)根据题意,由于用1、2、3、4、5、6、7可组成多少个无重复数字的四位数,且是偶数,那么末尾是偶数,有3种,其余的任意选择三个,即从剩下的6个总选3个排列即可,得到为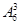 ,根据分步乘法计数原理可知为360
,根据分步乘法计数原理可知为360
(2)根据题意,由于用0、1、2、3、4、5可组成多少无重复数字的且可被5整除的五位数,那么额控制末尾数为0,或者5,需要分情况有零的情况和无零的情况,没有零,则总剩下的四个数字中任意选4个即可,有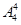 =24,而有零,则0不在首尾,末尾是5,和末尾是0,则所有的情况为
=24,而有零,则0不在首尾,末尾是5,和末尾是0,则所有的情况为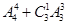 ,分布加法原理得到共有216
,分布加法原理得到共有216
考点:分步计数原理
点评:本题考查分步计数原理,是一个数字问题,数字问题是排列中的一大类问题,把排列问题包含在数字问题中,解题的关键是看清题目的实质,很多题目要分类讨论,要做到不重不漏


科目:高中数学 来源: 题型:解答题
从5名女同学和4名男同学中选出4人参加演讲比赛,分别按下列要求,各有多少种不同的选法?
(1)男、女同学各2名;
(2)男、女同学分别至少有1名;
(3)在(2)的前提下,男同学甲与女同学乙不能同时选出.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知甲、乙、丙等6人 .
(1)这6人同时参加一项活动,必须有人去,去几人自行决定,共有多少种不同的去法?
(2)这6人同时参加6项不同的活动,每项活动限1人参加,其中甲不参加第一项活动,乙不参加第三项活动,共有多少种不同的安排方法?
(3)这6人同时参加4项不同的活动,求每项活动至少有1人参加的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有4个不同的球,四个不同的盒子,把球全部放入盒内.
(1)共有多少种放法?
(2)恰有一个盒子不放球,有多少种放法?
(3)恰有一个盒内放2个球,有多少种放法?
(4)恰有两个盒不放球,有多少种放法?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用数字0、1、2、3组成3位数. 不允许数字重复.
①可以组成多少三位数?
②把①中的三位数按从小到大排序,230是第几个数?
③允许数字重复,可以组成多少个能被3整除的三位数.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,A地到火车站共有两条路径L1,L2,现随机抽取100位从A地到火车站的人进行调查,结果如下:
| 所用时间(min) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2人数 | 0 | 4 | 16 | 16 | 4 |
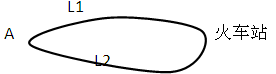
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)已知在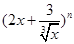 的展开式中,第
的展开式中,第 项的二项式系数与第2项的二项式系数的比为
项的二项式系数与第2项的二项式系数的比为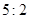 .(1)求
.(1)求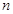 的值;(2)求含
的值;(2)求含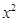 的项的系数;(3)求展开式中系数最大的项.
的项的系数;(3)求展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
由0,1,2,3,4,5这六个数字
(1)能组成多少个无重复数字的四位数?
(2)能组成多少个无重复数字的四位偶数?
(3)能组成多少个无重复数字且被25整除的四位数?
(4)组成无重复数字的四位数中比4032大的数有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com