
【题目】下图是把二进制的数11111(2)化成十进制数的﹣个程序框图,则判断框内应填入的条件是( ) 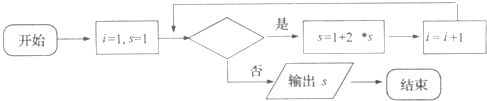
A.i≤4
B.i≤5
C.i>4
D.i>5
科目:高中数学 来源: 题型:
【题目】在△ABC中,a、b、c分别是角A、B、C的对边,如果a,b,c成等差数列,B=60°,△ABC的面积为3 ![]() ,那么b等于( )
,那么b等于( )
A.2 ![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与双曲线 ![]() ﹣
﹣ ![]() =1的两个焦点F1 , F2所连线段的和为6
=1的两个焦点F1 , F2所连线段的和为6 ![]() ,
,
(1)求动点P的轨迹方程;
(2)若 ![]()
![]() =0,求点P的坐标;
=0,求点P的坐标;
(3)求角∠F1PF2余弦值的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1),则a100等于( )
A.2×398
B.4×398
C.2×399
D.4×399
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,PA⊥平面ABC,AB=BC=AC=2,PA= ![]() ,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
,E,F分别是PB,BC的中点,则EF与平面PAB所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解学生遵守《中华人民共和国交通安全法》的情况,调查部门在某学校进行了如下的随机调查:向被调查者提出两个问题:(1)你的学号是奇数吗?(2)在过路口的时候你是否闯过红灯?要求被调查者背对调查人抛掷一枚硬币,如果出现正面,就回答第(1)个问题;否则就回答第(2)个问题.被调查者不必告诉调查人员自己回答的是哪一个问题,只需要回答“是”或“不是”,因为只有被调查本人知道回答了哪个问题,所以都如实做了回答.如果被调查的600人(学号从1到600)中有180人回答了“是”,由此可以估计在这600人中闯过红灯的人数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3+bx2+cx+d的图象如图,则函数y=ax2+ ![]() bx+
bx+ ![]() 的单调递增区间是( )
的单调递增区间是( ) 
A.(﹣∞,2]
B.![]() ,+∞)
,+∞)
C.[﹣2,3]
D.![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=1,a4=8,若a3 , a5分别为等差数列{bn}的第4项和第16项.
(1)求数列{an}﹑{bn}的通项公式;
(2)令cn=anbn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影O为AC的中点,A1O=2,AB⊥BC,AB=BC= ![]() 点P在线段A1B上,且cos∠PAO=
点P在线段A1B上,且cos∠PAO= ![]() ,则直线AP与平面A1AC所成角的正弦值为 .
,则直线AP与平面A1AC所成角的正弦值为 . 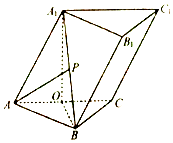
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com