
【题目】在![]() 中,
中,![]() ,则
,则![]() ____________.
____________.
【答案】![]()
【解析】
根据余弦定理化简![]() ,得到
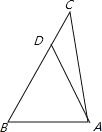
,得到![]() ;由题意,在BC上取D,使得BD=AD,连接AD,找出A﹣B,设BD=x,在△ADC中两次利用余弦定理将cos(A﹣B)及cosC表示出,分别求出x建立关于a,b的方程,化简变形后利用整体换元求出答案.
;由题意,在BC上取D,使得BD=AD,连接AD,找出A﹣B,设BD=x,在△ADC中两次利用余弦定理将cos(A﹣B)及cosC表示出,分别求出x建立关于a,b的方程,化简变形后利用整体换元求出答案.
由题意知,![]() 4cosC,
4cosC,
∴由余弦定理得,![]() 4
4![]() ,
,
化简可得![]() =2
=2![]() ,则
,则![]() ,
,
又![]() 中不妨设a>b,∴A>B.在BC上取D,使得BD=AD,连接AD,
中不妨设a>b,∴A>B.在BC上取D,使得BD=AD,连接AD,
设BD=x,则AD=x,DC=a﹣x,AC=b,
在△ADC中, cos∠DAC=cos(A﹣B)![]() ,
,
由余弦定理得:(a﹣x)2=x2+b2﹣2xb![]() ,
,
即:(b﹣6a)x=![]() ,
,
解得:x=![]() .①
.①
又在△ADC中,由余弦定理还可得cosC![]() ,
,
∴cosC![]() ,化简得x=
,化简得x=![]() ,②
,②
由①②可得![]() ,又
,又![]() =2
=2![]() ,
,
联立可得![]() =
=![]() ,即
,即![]() =
=![]() ,
,
两边同时除以![]() ,得
,得![]() =
=![]() +6,令
+6,令![]() ,则12
,则12![]() ,解得t=
,解得t=![]() 或
或![]() ,
,
又由题意![]() ,∴t=cosC
,∴t=cosC![]() =
=![]() ,
,
故答案为:![]() .
.


科目:高中数学 来源: 题型:
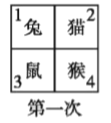
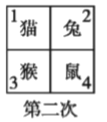
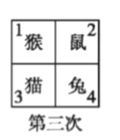
【题目】四个小动物换座位,开始是鼠、猴、兔、猫分别坐在 1,2,3,4 号位子上(如图), 第一次前后排动物互换座位,第二次左右列动物互换座位,.....,这样交替进行下去,那么第 2013 次互换座位后,小兔的座位对应的是( )

A. 编号 1 B. 编号 2 C. 编号 3 D. 编号 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.

(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据调查,某地区有300万从事传统农业的农民,人均年收入6000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有![]() 万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高
万人进企业工作,那么剩下从事传统农业的农民的人均年收入有望提高![]() ,而进入企业工作的农民的人均年收入为
,而进入企业工作的农民的人均年收入为![]() 元.
元.
(1)在建立加工企业后,多少农民进入企业工作,能够使剩下从事传统农业农民的总收入最大,并求出最大值;
(2)为了保证传统农业的顺利进行,限制农民加入加工企业的人数不能超过总人数的![]() ,当地政府如何引导农民,即
,当地政府如何引导农民,即![]() 取何值时,能使300万农民的年总收入最大.
取何值时,能使300万农民的年总收入最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有![]() ,
,![]() ,
,![]() ,
,![]() 四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
四件作品参加航模类作品比赛.已知这四件作品中恰有两件获奖.在结果揭晓前,甲、乙、丙、丁四位同学对这四件参赛作品的获奖情况预测如下:
甲说:“![]() 、
、![]() 同时获奖”;
同时获奖”;
乙说:“![]() 、
、![]() 不可能同时获奖”;
不可能同时获奖”;
丙说:“![]() 获奖”;
获奖”;
丁说:“![]() 、
、![]() 至少一件获奖”.
至少一件获奖”.
如果以上四位同学中有且只有二位同学的预测是正确的,则获奖的作品是( )
A. 作品![]() 与作品
与作品![]() B. 作品
B. 作品![]() 与作品
与作品![]() C. 作品
C. 作品![]() 与作品
与作品![]() D. 作品
D. 作品![]() 与作品
与作品![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列命题中,①![]() 的一个充要条件是
的一个充要条件是![]() 与它的共轭复数相等:
与它的共轭复数相等:
②利用独立性检验来考查两个分类变量![]() ,
,![]() 是否有关系,当随机变量
是否有关系,当随机变量![]() 的观测值
的观测值![]() 值越大,“
值越大,“![]() 与
与![]() 有关系”成立的可能性越大;
有关系”成立的可能性越大;
③在回归分析模型中,若相关指数越大,则残差平方和越小,模型的拟合效果越好;
④若![]() ,
,![]() 是两个相等的实数,则
是两个相等的实数,则![]() 是纯虚数;
是纯虚数;
⑤某校高三共有![]() 个班,
个班,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,由此推测各班都超过
人,由此推测各班都超过![]() 人,这个推理过程是演绎推理.
人,这个推理过程是演绎推理.
其中真命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线l:
,直线l:![]() ,设圆C的半径为1,圆心在l上.
,设圆C的半径为1,圆心在l上.
![]() 若圆心C也在直线
若圆心C也在直线![]() 上,过A作圆C的切线,求切线方程;
上,过A作圆C的切线,求切线方程;
![]() 若圆C上存在点M,使
若圆C上存在点M,使![]() ,求圆心C的横坐标a取值范围.
,求圆心C的横坐标a取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com