已知P={x|x2-8x-20≤0},Q={x||x-1|≤m},m∈R.
(1)若P∪Q=P,求实数m的取值范围;
(2)是否存在实数m,使得方程|x-1|=m至少有一个解x满足“x∈P”?若存在,求出m的取值范围;若不存在,说明理由.
解:P={x|x
2-8x-20≤0}=[-2,10],Q={x||x-1|≤m}=[1-m,1+m],
(1)∵P∪Q=P,则Q⊆P
①当Q=∅时,则m<0;
②当Q≠∅时,则
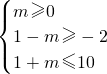
,解得0≤m≤3,
综合①②得m≤3;
(2)由方程|x-1|=m有解知:m≥0.
要使方程|x-1|=m的至少有一个解x满足“x∈P”,即|x-1|=m在区间[-2,10]上至少有一个实数解,
只需m≤9.
故m的取值范围为0≤m≤9.
分析:(1)根据已知条件,解一元二次不等式求得集合P,解绝对值不等式求得集合Q,根据P∪Q=P,可得Q⊆P,列出关于m的不等式组,解此不等式组即可求得结果,注意对空集的讨论;
(2)使得方程|x-1|=m至少有一个解x满足“x∈P”,即求方程|x-1|=m在区间[-2,10]上至少有一个实数解,转化为求函数y=|x-1|的值域,x∈[-2,10],即可求得结果.
点评:本题考查一元二次不等式的解法和绝对值不等式的解法,由P∪Q=P?Q⊆P,以及对∅的讨论是解问题(1)的关键;问题(2)的题意的理解和转化是解此题的关键,属中档题.

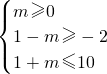 ,解得0≤m≤3,
,解得0≤m≤3,
