
���� ��1���������G��x��=2.8+x����R��x��=$\left\{\begin{array}{l}{-0.4{x}^{2}+4.2x��0��x��5}\\{0.05x+11��x��5}\end{array}\right.$��f��x��=R��x��-G��x������д��������y=f��x���Ľ���ʽ��
��2����x��5ʱ���ɺ���f��x���ݼ���֪f��x����f��5��=3.45����Ԫ������0��x��5ʱ������f��x��=-0.4��x-4��2+3.6����x=4ʱ��f��x�������ֵΪ3.6����Ԫ�����ɴ������������������̨��Ʒʱ����ʹӯ����࣮
��� �⣺��1���������G��x��=2.8+x��
��R��x��=$\left\{\begin{array}{l}{-0.4{x}^{2}+4.2x��0��x��5}\\{0.05x+11��x��5}\end{array}\right.$��
��f��x��=R��x��-G��x��=$\left\{\begin{array}{l}{-0.4{x}^{2}+3.2x-2.8��0��x��5}\\{8.2-0.95x��x��5}\end{array}\right.$��
��2����x��5ʱ���ߺ���f��x���ݼ�����f��x����f��5��=3.45����Ԫ����
��0��x��5ʱ������f��x��=-0.4��x-4��2+3.6��
���Ե�x=4ʱ��f��x�������ֵΪ3.6����Ԫ����
���Ե���������4��̨��Ʒʱ����ʹӮ����������ֵΪ3.6��Ԫ��
���� �����ۺϿ������ܳɱ�=�̶��ɱ�+�����ɱ�������=��������-�ܳɱ����ֶκ��������ʡ����κ�����һ�κ����ĵ����ԵȻ���֪ʶ����������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��A��B��C��˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0���ϵ������㣬AB����ԭ��O��AC�����ҽ���F����BF��AC��|BF|=|CF|�����˫���ߵ���������$\frac{{\sqrt{10}}}{2}$��
��ͼ��ʾ��A��B��C��˫����$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0���ϵ������㣬AB����ԭ��O��AC�����ҽ���F����BF��AC��|BF|=|CF|�����˫���ߵ���������$\frac{{\sqrt{10}}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
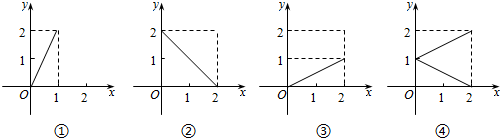
| A�� | �٢ڢۢ� | B�� | �٢ڢ� | C�� | �ڢ� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com