
【题目】已知函数f(x)=x2+mx+n有两个零点﹣1与3.
(1)求出函数f(x)的解析式,并指出函数f(x)的单调递增区间;
(2)若g(x)=f(|x|)在x1 , x2∈[t,t+1]是增函数,求实数t的取值范围.
【答案】
(1)解:函数f(x)=x2+mx+n有两个零点﹣1与3,由韦达定理,可得:m=﹣2,n=﹣3,
故得函数f(x)的解析式f(x)=x2﹣2x﹣3,
解析式化简得f(x)=(x﹣1)2﹣4.
对称轴x=1,
∴f(x)的增区为(1,+∞)
(2)解:∵g(x)=f(|x|),由(1)得f(x)=x2﹣2x﹣3
∴g(x)=x2﹣2|x|﹣3
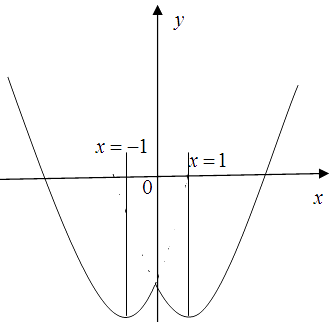
画g(x)的图象如下:
由图象可知:[﹣1,0]和[1,+∞)是单调递增区间;
∵函数g(x)要使[t,t+1]是增函数,
由图观察可得:t=﹣1或t≥1.
故得实数t的取值范围是{t|t=﹣1或t≥1}.
【解析】(1)函数有两个零点﹣1与3,由韦达定理可求解m,n的值,可得函数f(x)的解析式,利用二次函数的性质可得单调性.(2)求出g(x)的解析式,画出图形,数形结合可求得t的取值范围.
【考点精析】关于本题考查的函数单调性的判断方法,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】一个袋子内装有2个绿球,3个黄球和若干个红球(所有球除颜色外其他均相同),从中一次性任取2个球,每取得1个绿球得5分,每取得1个黄球得2分,每取得1个红球得1分,用随机变量![]() 表示2个球的总得分,已知得2分的概率为
表示2个球的总得分,已知得2分的概率为![]() .
.
(Ⅰ)求袋子内红球的个数;
(Ⅱ)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,且函数
,且函数![]() .
.
(Ⅰ)当函数![]() 在
在![]() 上的最大值为3时,求
上的最大值为3时,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若对任意的![]() ,函数
,函数![]() ,
, ![]() 的图像与直线
的图像与直线![]() 有且仅有两个不同的交点,试确定
有且仅有两个不同的交点,试确定![]() 的值.并求函数
的值.并求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
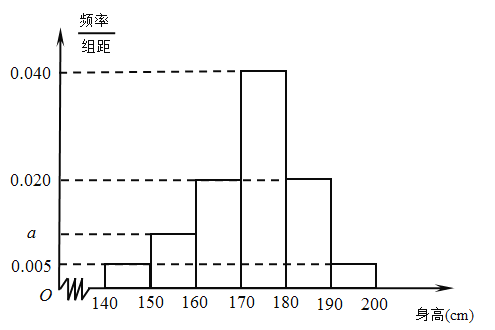
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)假设同组中的每个数据用该组区间的中点值代替,估计该市中学生中的全体男生的平均身高;
(Ⅲ)从该市的中学生中随机抽取一名男生,根据直方图中的信息,估计其身高在180 cm 以上的概率.若从全市中学的男生(人数众多)中随机抽取![]() 人,用
人,用![]() 表示身高在
表示身高在![]() 以上的男生人数,求随机变量
以上的男生人数,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为I的函数y=f(x),如果存在区间[m,n]I,同时满足:
①f(x)在[m,n]内是单调函数;
②当定义域是[m,n],f(x)值域也是[m,n],则称[m,n]是函数y=f(x)的“好区间”.
(1)设g(x)=loga(ax﹣2a)+loga(ax﹣3a)(其中a>0且a≠1),求g(x)的定义域并判断其单调性;
(2)试判断(1)中的g(x)是否存在“好区间”,并说明理由;
(3)已知函数P(x)= ![]() (t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
(t∈R,t≠0)有“好区间”[m,n],当t变化时,求n﹣m 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数,当x≥0时,f(x)= 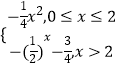 ,若关于x的方程[f(x)]2+af(x)+
,若关于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
=0,a∈R有且仅有8个不同实数根,则实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在区间[0,a]上的函数f(x)的图象如图所示,记以A(0,f(0)),B(a,f(a)),C(x,f(x))为顶点的三角形的面积为S(x),则函数S(x)的导函数S′(x)的图象大致是( ) 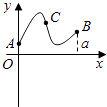
A.
B.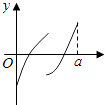
C.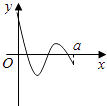
D.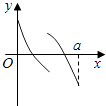
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+(1﹣a) x2﹣a(a+2)x+b(a,b∈R).
(1)若函数f(x)的图象过原点,且在原点处的切线斜率是﹣3,求a,b的值;
(2)若函数f(x)在区间(﹣1,1)上不单调,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com