
先阅读下列不等式的证法,再解决后面的问题:
已知![]()
证明:构造函数![]()
即![]()
因为对一切![]() ,恒有
,恒有![]() ,所以
,所以![]() 从而得
从而得![]()
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请写出上述问题的推广式.
(2)对推广的问题加以证明.
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:高中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:阅读理解
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
先阅读下列不等式的证法,再解决后面的问题:已知![]() ,
,![]() ,求证
,求证![]() .
.
证明:构造函数![]() ,
,![]()
因为对一切![]() ,恒有
,恒有![]() ≥0,所以
≥0,所以![]() ≤0,从而得
≤0,从而得![]() ,
,
(1)若![]() ,
,![]() ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源:2010-2011年福建省高二下学期学段考试数学理卷 题型:解答题
(本小题15分)
先阅读下列不等式的证法,再解决后面的问题:已知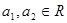 且
且 ,求证
,求证
证明:构造函数 因为对一切
因为对一切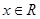 ,恒有
,恒有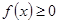 ,所以
,所以 4-8
4-8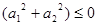 ,从而
,从而
(1)若 ,且
,且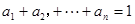 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述证法,对你的结论加以证明;
(3)若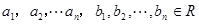 ,求证
,求证
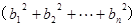
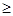
 .[
.[
查看答案和解析>>
科目:高中数学 来源:2009-2010学年度新课标高三上学期数学单元测试12-理科-算法、复数、推理与证明 题型:解答题
先阅读下列不等式的证法,再解决后面的问题:已知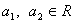 ,
,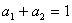 ,求证
,求证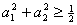 .
.
证明:构造函数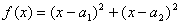 ,
,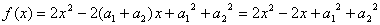
因为对一切 ,恒有
,恒有 ≥0,所以
≥0,所以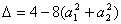 ≤0,从而得
≤0,从而得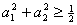 ,
,
(1)若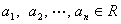 ,
,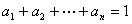 ,请写出上述结论的推广式;
,请写出上述结论的推广式;
(2)参考上述解法,对你推广的结论加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com