
分析 (1)a=-1,B={x|-2≤x≤1},即可求A∩B和A∪B;
(2)由A∩B=B,得B⊆A,然后分B为∅何B不为∅讨论,当B不是∅时,由两集合端点值间的关系列不等式组求得a的取值范围.
解答 解:(1)a=-1,B={x|-2≤x≤1}.
∴A∩B={x|-2≤x≤-1},A∪B={x|x≤1或x≥5};
(2)由A∩B=B,得B⊆A,
若2a>a+2,即a>2,B=∅,满足B⊆A;
当2a≤a+2,即a≤2时,要使B⊆A,
则a+2≤-1或2a≥5,解得a≤-3.
∴使A∩B=B的a的取值范围是a≤-3或a>2.
点评 本题考查了交集及其运算,考查了分类讨论的解题思想方法,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3π}{4}$ | B. | $\frac{4π}{3}$ | C. | $\frac{5π}{3}$ | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
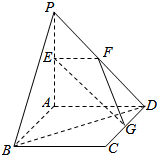 平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点
平面PAD⊥平面ABCD,ABCD为正方形,△PAD是直角三角形,且PA=PD=2,E,F,G分别是线段PA,PD,CD的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧(¬q) | B. | p∨(¬q) | C. | p∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,$sinB=\frac{{3\sqrt{6}}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,$sinB=\frac{{3\sqrt{6}}}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com