
(本小题满分13分)
某商场根据调查,估计家电商品从年初(1月)开始的 个月内累计的需求量
个月内累计的需求量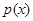 (百件)为
(百件)为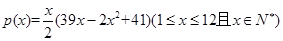
(1)求第 个月的需求量
个月的需求量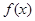 的表达式.
的表达式.
(2)若第 个月的销售量满足
个月的销售量满足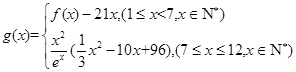 (单位:百件),每件利润
(单位:百件),每件利润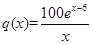 元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少?
元,求该商场销售该商品,求第几个月的月利润达到最大值?最大是多少? 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本题满分10分)
已知函数f (x)=| x-a | + | x + 2 |(a为常数,且a∈R).
(Ⅰ)若函数f (x)的最小值为2,求a的值;
(Ⅱ)当a=2时,解不等式f (x)≤6.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com