
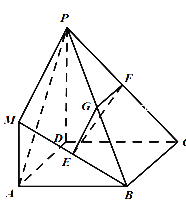
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,且
的中点,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】在![]() 中,已知(sin A+sin B+sin C)·(sin B+sin C-sin A)=3sin Bsin C.
中,已知(sin A+sin B+sin C)·(sin B+sin C-sin A)=3sin Bsin C.
(Ⅰ)求角A的值;
(Ⅱ)求![]() sin B-cos C的最大值.
sin B-cos C的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}和{bn}的每一项都是正数,且a1=8,b1=16,且an , bn , an+1成等差数列,bn , an+1 , bn+1成等比数列.
(1)求a2 , b2的值;
(2)求数列{an},{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有以下命题:
①对任意的α∈R都有sin3α=3sinα﹣4sin3α成立;
②对任意的△ABC都有等式a=bcosA+ccosB成立;
③满足“三边是连续的三个正整数且最大角是最小的2倍”的三角形存在且唯一;
④若A,B是钝角△ABC的二锐角,则sinA+sinB<cosA+cosB.
其中正确的命题的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=tx2-(22t+60)x+144t(x>0).
(1)要使f(x)≥0恒成立,求t的最小值;
(2)令f(x)=0,求使t>20成立的x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心为原点
的中心为原点![]() ,离心率
,离心率![]() ,其中一个焦点的坐标为
,其中一个焦点的坐标为![]()
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)当点![]() 在椭圆
在椭圆![]() 上运动时,设动点
上运动时,设动点![]() 的运动轨迹为
的运动轨迹为![]() 若点
若点![]() 满足:
满足: ![]() 其中
其中![]() 是
是![]() 上的点.直线
上的点.直线![]() 的斜率之积为
的斜率之积为![]() ,试说明:是否存在两个定点
,试说明:是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个不透明的箱子,每个箱子都装有4个完全相同的小球,球上分别标有数字1,2,3,4.
(1)甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
(2)摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x的图象向右平移φ(0<φ< ![]() )个单位后得到函数g(x)的图象,若对满足|f(x1)﹣g(x2)|=2的x1、x2有|x1﹣x2|min=
)个单位后得到函数g(x)的图象,若对满足|f(x1)﹣g(x2)|=2的x1、x2有|x1﹣x2|min= ![]() ,则φ= .
,则φ= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com