
【题目】某蔬菜批发商经销某种新鲜蔬菜(以下简称![]() 蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的
蔬菜),购入价为200元/袋,并以300元/袋的价格售出,若前8小时内所购进的![]() 蔬菜没有售完,则批发商将没售完的
蔬菜没有售完,则批发商将没售完的![]() 蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把
蔬菜以150元/袋的价格低价处理完毕(根据经验,2小时内完全能够把![]() 蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天
蔬菜低价处理完,且当天不再购进).该蔬菜批发商根据往年的销量,统计了100天![]() 蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.
蔬菜在每天的前8小时内的销售量,制成如下频数分布条形图.

(1)若某天该蔬菜批发商共购入6袋![]() 蔬菜,有4袋
蔬菜,有4袋![]() 蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
蔬菜在前8小时内分别被4名顾客购买,剩下2袋在8小时后被另2名顾客购买.现从这6名顾客中随机选2人进行服务回访,则至少选中1人是以150元/袋的价格购买的概率是多少?
(2)以上述样本数据作为决策的依据.
(i)若今年![]() 蔬菜上市的100天内,该蔬菜批发商坚持每天购进6袋
蔬菜上市的100天内,该蔬菜批发商坚持每天购进6袋![]() 蔬菜,试估计该蔬菜批发商经销
蔬菜,试估计该蔬菜批发商经销![]() 蔬菜的总盈利值;
蔬菜的总盈利值;
(ii)若明年该蔬菜批发商每天购进![]() 蔬菜的袋数相同,试帮其设计明年的
蔬菜的袋数相同,试帮其设计明年的![]() 蔬菜的进货方案,使其所获取的平均利润最大.
蔬菜的进货方案,使其所获取的平均利润最大.
【答案】(1)![]() ;(2)(i)
;(2)(i)![]() 元;(ii)该批发商明年每天购进
元;(ii)该批发商明年每天购进![]() 蔬菜5袋,所获平均利润最大.
蔬菜5袋,所获平均利润最大.
【解析】
(1)通过列举分别求出“从6人中任选2人”和“至少选中1人是以150元/袋的价格购买”的基本事件个数,通过古典概型公式计算即可;
(2)(i)通过频数分布条形图进行估算即可;(ii)分别计算购进![]() 蔬菜4袋、5袋、6袋时的每天所获平均利润,比较大小即可.
蔬菜4袋、5袋、6袋时的每天所获平均利润,比较大小即可.
(1)设这6人中花150元/袋的价格购买![]() 蔬菜的顾客为
蔬菜的顾客为![]() ,
,
其余4人为![]() ,
,![]() ,
,![]() ,
,![]() .
.
则从6人中任选2人的基本事件为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15个.
,共15个.
其中至少选中1人是以150元/袋的价格购买的基本事件有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共9个.
,共9个.
![]() 至少选中1人是以150元/袋的价格购买的概率为
至少选中1人是以150元/袋的价格购买的概率为![]() .
.
(2)(i)该蔬菜批发商经销![]() 蔬菜的总盈利值为:
蔬菜的总盈利值为:![]() (元).
(元).
(ii)当购进![]() 蔬菜4袋时,每天所获平均利润为
蔬菜4袋时,每天所获平均利润为![]() (元),
(元),
当购进![]() 蔬菜5袋时,每天所获平均利润为
蔬菜5袋时,每天所获平均利润为![]() (元)
(元)
当购进![]() 蔬菜6袋时,每天所获平均利润为
蔬菜6袋时,每天所获平均利润为![]() (元)
(元)
综上,该批发商明年每天购进![]() 蔬菜5袋,所获平均利润最大.
蔬菜5袋,所获平均利润最大.


科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记[x]为不超过实数x的最大整数,例如,[2]=2,[1.5]=1,[-0.3]=-1.设a为正整数,数列{xn}满足x1=a,xn+1=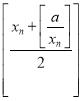 (n∈N*).现有下列命题:
(n∈N*).现有下列命题:
①当a=5时,数列{xn}的前3项依次为5,3,2;
②对数列{xn}都存在正整数k,当n≥k时总有xn=xk;
③当n≥1时,xn>![]() -1;
-1;
④对某个正整数k,若xk+1≥xk,则xk=[![]() ].
].
其中的真命题有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,ABCD为矩形,
中,ABCD为矩形,![]() 是以
是以![]() 为直角的等腰直角三角形,平面
为直角的等腰直角三角形,平面![]() 平面ABCD.
平面ABCD.

(1)证明:平面![]() 平面PBC;
平面PBC;
(2)![]() 为直线PC的中点,且
为直线PC的中点,且![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北武汉市发现多起病毒性肺炎病例,并迅速在全国范围内开始传播,专家组认为,本次病毒性肺炎病例的病原体初步判定为新型冠状病毒,该病毒存在人与人之间的传染,可以通过与患者的密切接触进行传染.我们把与患者有过密切接触的人群称为密切接触者,每位密切接触者被感染后即被称为患者.已知每位密切接触者在接触一个患者后被感染的概率为![]() ,某位患者在隔离之前,每天有
,某位患者在隔离之前,每天有![]() 位密切接触者,其中被感染的人数为
位密切接触者,其中被感染的人数为![]() ,假设每位密切接触者不再接触其他患者.
,假设每位密切接触者不再接触其他患者.
(1)求一天内被感染人数为![]() 的概率
的概率![]() 与
与![]() 、
、![]() 的关系式和
的关系式和![]() 的数学期望;
的数学期望;
(2)该病毒在进入人体后有14天的潜伏期,在这14天的潜伏期内患者无任何症状,为病毒传播的最佳时间,设每位患者在被感染后的第二天又有![]() 位密切接触者,从某一名患者被感染,按第1天算起,第
位密切接触者,从某一名患者被感染,按第1天算起,第![]() 天新增患者的数学期望记为
天新增患者的数学期望记为![]() .
.
(i)求数列![]() 的通项公式,并证明数列
的通项公式,并证明数列![]() 为等比数列;
为等比数列;
(ii)若戴口罩能降低每位密切接触者患病概率,降低后的患病概率![]() ,当
,当![]() 取最大值时,计算此时
取最大值时,计算此时![]() 所对应的
所对应的![]() 值和此时
值和此时![]() 对应的
对应的![]() 值,根据计算结果说明戴口罩的必要性.(取
值,根据计算结果说明戴口罩的必要性.(取![]() )
)
(结果保留整数,参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定椭圆![]() >
>![]() >0
>0![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“准圆”.若椭圆
的“准圆”.若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上的一个端点到
,其短轴上的一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程和其“准圆”方程;
的方程和其“准圆”方程;
(2)点![]() 是椭圆
是椭圆![]() 的“准圆”上的一个动点,过点
的“准圆”上的一个动点,过点![]() 作直线
作直线![]() ,使得
,使得![]() 与椭圆
与椭圆![]() 都只有一个交点.求证:
都只有一个交点.求证:![]() ⊥
⊥![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2017年1月至2019年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是( )
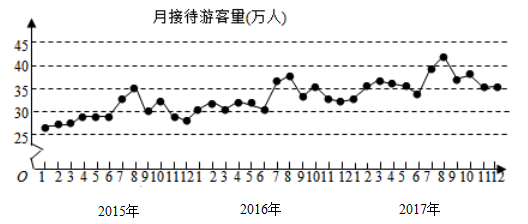
A.年接待游客量逐年增加
B.各年的月接待游客量高峰期大致在8月
C.2017年1月至12月月接待游客量的中位数为30万人
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com