
【题目】已知![]() 是无穷等比数列,若
是无穷等比数列,若![]() 的每一项都等于它后面所有项的
的每一项都等于它后面所有项的![]() 倍,则实数
倍,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】(﹣∞,﹣2]∪(0,+∞).
【解析】
无穷等比数列{an}的各项和为A,前n项和为Sn,公比为q,0<|q|≤1,q≠1.可得A![]() ,Sn
,Sn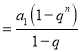 ,由题意可得:an=k(A﹣Sn),代入化为:k
,由题意可得:an=k(A﹣Sn),代入化为:k![]() ,分类讨论即可得出.
,分类讨论即可得出.
解:无穷等比数列{an}的各项和为A,前n项和为Sn,公比为q,0<|q|≤1,q≠1.
则A![]() ,Sn
,Sn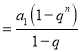 ,
,
由题意可得:an=k(A﹣Sn),
∴a1q=k(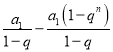 ),
),
化为:k![]() ,
,
1>q>0时,k>0,n→+∞时,k→+∞.
﹣1≤q<0时,可得:n为偶数时,k∈(﹣∞,﹣2];n为奇数时,k>0.
∴k∈(﹣∞,﹣2]∪(0,+∞).
综上可得:k∈(﹣∞,﹣2]∪(0,+∞).
故答案为:(﹣∞,﹣2]∪(0,+∞).


科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,对任意
,对任意![]() ,有
,有![]() 成立.
成立.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,
,![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,求正整数
项和,求正整数![]() ,使得对任意
,使得对任意![]() ,
,![]() 恒成立;
恒成立;
(3)设![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意
项和,若对任意![]() 均有
均有![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某小区为美化环境,准备在小区内的草坪的一侧修建一条直路OC,另一侧修建一条休闲大道.休闲大道的前一段OD是函数![]() 的图象的一部分,后一段DBC是函数
的图象的一部分,后一段DBC是函数![]() 的图象,图象的最高点为
的图象,图象的最高点为 ,且
,且![]() ,垂足为点F.
,垂足为点F.

(1)求函数![]() 的解析式;
的解析式;
(2)若在草坪内修建如图所示的矩形儿童乐园PMFE,点P在曲线OD上,其横坐标为![]() ,点E在OC上,求儿童乐园的面积.
,点E在OC上,求儿童乐园的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表提供了工厂技术改造后某种型号设备的使用年限![]() 和所支出的维修费
和所支出的维修费![]() (万元)的几组对照数据:
(万元)的几组对照数据:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
参考公式: ,
,![]() .
.
(1)若知道![]() 对
对![]() 呈线性相关关系,请根据上表提供的数据,用最小二乘法求出
呈线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该工厂技术改造前该型号设备使用10年的维修费用为9万元,试根据(1)求出的线性回归方程,预测该型号设备技术改造后,使用10年的维修费用能否比技术改造前降低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油![]() 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为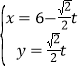 (t是参数),在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为
(t是参数),在以坐标原点为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
(Ⅰ)写出直线l的普通方程、曲线C的参数方程;
(Ⅱ)过曲线C上任意一点A作与直线l的夹角为45°的直线,设该直线与直线l交于点B,求![]() 的最值.
的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 的左、右焦点为
的左、右焦点为![]() ,
,![]() ,
,![]() 为
为![]() 右支上的动点(非顶点),
右支上的动点(非顶点),![]() 为
为![]() 的内心.当
的内心.当![]() 变化时,
变化时,![]() 的轨迹为( )
的轨迹为( )
A.直线的一部分B.椭圆的一部分
C.双曲线的一部分D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com