
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在下图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示. 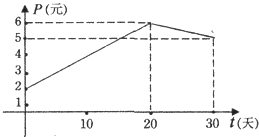
第t天 | 4 | 10 | 16 | 22 |
Q(万股) | 36 | 30 | 24 | 18 |
(1)根据提供的图象,写出该种股票每股交易价格P(元)与时间t(天)所满足的函数关系式;
(2)根据表中数据确定日交易量Q(万股)与时间t(天)的一次函数关系式;
(3)在(2)的结论下,用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求出这30天中第几日交易额最大,最大值为多少?
【答案】
(1)解: 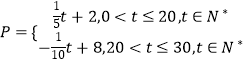
(2)解:设Q=at+b(a,b为常数),将(4,36)与(10,30)的坐标代入,
得 ![]() .
.
日交易量Q(万股)与时间t(天)的一次函数关系式为Q=40﹣t,0<t≤30,t∈N*
(3)解:由(1)(2)可得 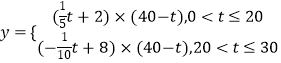
即 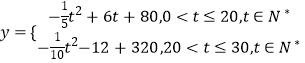
当0<t≤20时,当t=15时,ymax=125;
当 ![]() 上是减函数,y<y(20)<y(15)=125.
上是减函数,y<y(20)<y(15)=125.
所以,第15日交易额最大,最大值为125万元
【解析】(1)根据图象可知此函数为分段函数,在(0,20]和(20,30]两个区间利用待定系数法分别求出一次函数关系式联立可得P的解析式;(2)因为Q与t成一次函数关系,根据表格中的数据,取出两组即可确定出Q的解析式;(3)根据股票日交易额=交易量×每股较易价格可知y=PQ,可得y的解析式,分别在各段上利用二次函数求最值的方法求出即可.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
【题目】已知点A(2,0),点B(﹣2,0),直线l:(λ+3)x+(λ﹣1)y﹣4λ=0(其中λ∈R).
(1)求直线l所经过的定点P的坐标;
(2)若直线l与线段AB有公共点,求λ的取值范围;
(3)若分别过A,B且斜率为 ![]() 的两条平行直线截直线l所得线段的长为4
的两条平行直线截直线l所得线段的长为4 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x , 函数g(x)=log
)x , 函数g(x)=log ![]() x.
x.
(1)若g(ax2+2x+1)的定义域为R,求实数a的取值范围;
(2)当x∈[( ![]() )t+1 , (
)t+1 , ( ![]() )t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
)t]时,求函数y=[g(x)]2﹣2g(x)+2的最小值h(t);
(3)是否存在非负实数m,n,使得函数y=log ![]() f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
f(x2)的定义域为[m,n],值域为[2m,2n],若存在,求出m,n的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣4x+a+3,g(x)=mx+5﹣2m
(1)当a=﹣3,m=0时,求方程f(x)﹣g(x)=0的解;
(2)若方程f(x)=0在[﹣1,1]上有实数根,求实数a的取值范围;
(3)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知销售“笔记本电脑”和“台式电脑”所得的利润分别是P(单位:万元)和Q(单位:万元),它们与进货资金t(单位:万元)的关系有经验公式P= ![]() t和Q=
t和Q= ![]()
![]() .某商场决定投入进货资金50万元,全部用来购入这两种电脑,那么该商场应如何分配进货资金,才能使销售电脑获得的利润y(单位:万元)最大?最大利润是多少万元?
.某商场决定投入进货资金50万元,全部用来购入这两种电脑,那么该商场应如何分配进货资金,才能使销售电脑获得的利润y(单位:万元)最大?最大利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
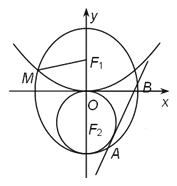
【题目】已知![]() 分别为椭圆
分别为椭圆![]() 的上、下焦点,
的上、下焦点, ![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是
是![]() 与
与![]() 在第二象限的交点,且
在第二象限的交点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)与圆![]() 相切的直线
相切的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,
若椭圆![]() 上一点
上一点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() ,x∈R.
,x∈R.
(1)求证:对一切实数x,f(x)=f(1﹣x)恒为定值.
(2)计算:f(﹣6)+f(﹣5)+f(﹣4)+f(﹣3)+…+f(0)+…+f(6)+f(7).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com