
【题目】如图,在三棱锥![]() 中,
中,![]() ⊥底面
⊥底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
已知![]() ,
,![]() ,
,![]() ,
,![]() .求:
.求:
(1)三棱锥PABC的体积;
(2)异面直线BC与AD所成角的余弦值.

 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的一个焦点,过原点的直线
的一个焦点,过原点的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() ,
, ![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() ,过点
,过点![]() 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于![]() 两点,线段
两点,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一网站营销部为统计某市网友2017年12月12日在某网店的网购情况,随机抽查了该市60名网友在该网店的网购金额情况,如表:
网购金额 (单位:千元) | 频数 | 频率 |
| 3 |
|
|
|
|
| 9 |
|
| 15 |
|
| 18 |
|
|
|
|
合计 | 60 |
|
若将当日网购金额不小于2千元的网友称为“网购达人”,网购金额小于2千元的网友称为“网购探者”,已知“网购达人”与“网购探者”人数的比例为![]() .
.
(1)确定![]() ,
,![]() ,
,![]() ,
,![]() 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;
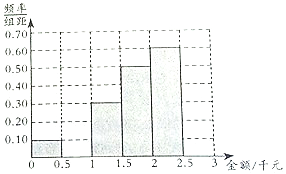
(2)试根据频率分布直方图估算这60名网友当日在该网店网购金额的平均数和中位数;若平均数和中位数至少有一个不低于2千元,则该网店当日评为“皇冠店”,试判断该网店当日能否被评为“皇冠店”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4﹣1几何证明选讲】
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BCAE=DCAF,B、E、F、C四点共圆.
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() =l (a>b>0)的焦距为2,离心率为
=l (a>b>0)的焦距为2,离心率为 ![]() ,椭圆的右顶点为A.
,椭圆的右顶点为A.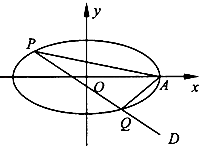
(1)求该椭圆的方程:
(2)过点D( ![]() ,﹣
,﹣ ![]() )作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二阶矩阵M有特征值λ=8及对应的一个特征向量 ![]() =[
=[ ![]() ],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
],并且矩阵M对应的变换将点(﹣1,2)变换成(﹣2,4).
(1)求矩阵M;
(2)求矩阵M的另一个特征值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读如下程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( ) 
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过
经过![]() ,且椭圆
,且椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设斜率存在的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 为坐标原点,
为坐标原点,![]() ,且
,且![]() 与圆心为
与圆心为![]() 的定圆
的定圆![]() 相切.直线
相切.直线![]() :
:![]() (
(![]() )与圆
)与圆![]() 交于
交于![]() 两点,
两点,![]() .求
.求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com