
����Ŀ����װ������2017����д��������������㣬�ò�Ʒ���������������ó����������![]() ��������������
��������������![]() ��
��![]() ����Ԫ����
����Ԫ����![]() .��֪
.��֪![]() �������ò�Ʒ�Ĺ̶�Ͷ��Ϊ
�������ò�Ʒ�Ĺ̶�Ͷ��Ϊ![]() ��Ԫ��ÿ����
��Ԫ��ÿ����![]() ����ò�Ʒ��ҪͶ��
����ò�Ʒ��ҪͶ��![]() ��Ԫ.���ҽ�ÿ����Ʒ�����ۼ۸�Ϊÿ����Ʒ��ƽ���ɱ���
��Ԫ.���ҽ�ÿ����Ʒ�����ۼ۸�Ϊÿ����Ʒ��ƽ���ɱ���![]() ������Ʒ�ɱ������̶�Ͷ�����Ͷ���������ʽ𣬲������������ã�.
������Ʒ�ɱ������̶�Ͷ�����Ͷ���������ʽ𣬲������������ã�.
��1����2017��ò�Ʒ������![]() ��Ԫ��ʾΪ���������
��Ԫ��ʾΪ���������![]() ��Ԫ�ĺ�����
��Ԫ�ĺ�����
��2���÷�װ��2017��Ĵ�������Ͷ�������Ԫʱ���������
���𰸡���1��![]() ��
��![]() ������2��������
������2��������
�����������������
��1��������֪��ÿ����Ʒ�����ۼ۸�Ϊ![]() �����ɱ�ʾ������
�����ɱ�ʾ������![]() ���ڴ�������
���ڴ�������![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
��2���ɣ�1���еĺ�����ϵʽ�����û�������ʽ����ֵ�����ɵó�2017��������ö���ʱ���������.
���������
��1��������֪��ÿ����Ʒ�����ۼ۸�Ϊ![]()
����![]()
![]()
![]()
![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��
��2����![]()
![]()
![]()
���ҽ���![]() ����
����![]() ʱȡ�Ⱥ�.
ʱȡ�Ⱥ�.
��![]()
��![]() ʱ����
ʱ����![]() ʱ��
ʱ�� ![]() �����ֵ��
�����ֵ��
��![]() ʱ����֤
ʱ����֤![]() ����
����![]() ������������
Ϊ������������![]() ʱ��
ʱ�� ![]() �����ֵ��
�����ֵ��
�𣺵�![]() ʱ���÷�װ��2017��Ĵ�������Ͷ��
ʱ���÷�װ��2017��Ĵ�������Ͷ��![]() ��Ԫʱ���������
��Ԫʱ���������
��![]() ʱ���÷�װ��2017��Ĵ�������Ͷ��
ʱ���÷�װ��2017��Ĵ�������Ͷ��![]() ��Ԫʱ���������.
��Ԫʱ���������.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��ƽ���ı���![]() �У�
�� ![]() ��
�� ![]() ���ֽ�
���ֽ�![]() ��
��![]() ���𣬵õ�����
���𣬵õ�����![]() ����ͼ2������
����ͼ2������![]() ����
����![]() ����
Ϊ����![]() ���е�.
���е�.
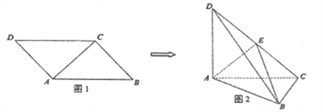
��1����֤�� ![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �������
�������
��3����![]() �Ľ�ƽ�������Ƿ���ڵ�
�Ľ�ƽ�������Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() �������ڣ���
�������ڣ���![]() �ij����������ڣ���˵������.
�ij����������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ������
������![]() �DZ߳�Ϊ2�����Σ�
�DZ߳�Ϊ2�����Σ� ![]() ����
����![]() ƽ��
ƽ��![]() .
.

��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() �ļн�Ϊ
�ļн�Ϊ![]() �������߶�
�������߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������費��ʽ![]() ������
������![]() ��һ��ʵ��
��һ��ʵ��![]() ��ȡֵ����������
��ȡֵ����������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�����Ƿ����ʵ��![]() ,ʹ�ò���ʽ
,ʹ�ò���ʽ![]() ������
������![]() ��һ��ʵ��
��һ��ʵ��![]() ��ȡֵ��������
��ȡֵ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����
����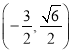 ��˳��������Բ���ĸ�����õ����ı��ε����Ϊ
��˳��������Բ���ĸ�����õ����ı��ε����Ϊ![]() ����
����![]() .
.
��������Բ![]() �ķ���.
�ķ���.
������֪��![]() ������Բ
������Բ![]() �ϵ�����.
�ϵ�����.
��������![]() ����
����![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() �������
�������
��������![]() ��֤����
��֤���� ![]() ������Ϊ�ȱ�������.
������Ϊ�ȱ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�ӿ�����Դ������ҵ��չ���ƽ����ܼ��ţ����Ҷ������߹�������Դ�������貹�������жԴ��綯�˳����������±���

ijУ�о���ѧϰС�飬�������г������ѡȡ��![]() �����綯���ó�����������ʻ���
�����綯���ó�����������ʻ���![]() �����γ�������ʻ�������̣�������Ƶ����Ƶ����ͳ�Ʊ���
�����γ�������ʻ�������̣�������Ƶ����Ƶ����ͳ�Ʊ���

��1����![]() ��ֵ��
��ֵ��
��2��������![]() �����綯���ó�����ѡ3������ѡ����3������ʻ��̶�������180����ĸ��ʣ�
�����綯���ó�����ѡ3������ѡ����3������ʻ��̶�������180����ĸ��ʣ�
��3�������Ƶ����Ϊ���ʣ���ij��ͥ��ij�������۹�˾������2�����綯���ó�����ü�ͥ��õIJ���Ϊ![]() ����λ����Ԫ������
����λ����Ԫ������![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD��A1B1C1D1�У�AB=2��AA1=AD=4����EΪAB�е㣮
��1����֤��BD1��ƽ��A1DE��
��2����֤��A1D��ƽ��ABD1 �� 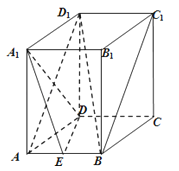
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ե�C��t��![]() �� ��t��R��t��0��ΪԲ�ĵ�Բ��x�ύ�ڵ�O��A����y�ύ�ڵ�O��B������OΪԭ�㣮
�� ��t��R��t��0��ΪԲ�ĵ�Բ��x�ύ�ڵ�O��A����y�ύ�ڵ�O��B������OΪԭ�㣮
��1����֤����AOB�����Ϊ��ֵ��
��2����ֱ��2x+y��4=0��ԲC���ڵ�M��N����OM=ON����ԲC�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�ļ������У��ı���ABCD�Ǿ��Σ�ƽ��ABCD��ƽ��ABE����֪AB=2��AE=BE= ![]() ���ҵ��涨����ͼ����ֱƽ��ABCDʱ���ü�����IJ���ͼ�����Ϊ
���ҵ��涨����ͼ����ֱƽ��ABCDʱ���ü�����IJ���ͼ�����Ϊ ![]() ����M��N�ֱ����߶�DE��CE�ϵĶ��㣬��AM+MN+NB����СֵΪ
����M��N�ֱ����߶�DE��CE�ϵĶ��㣬��AM+MN+NB����СֵΪ 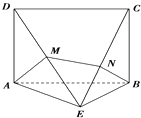
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com