
 ,点
,点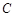 是圆
是圆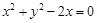 上任意一点,则
上任意一点,则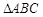 面积的最小值是( ).
面积的最小值是( ).A.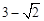 | B.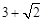 | C.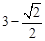 | D.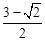 |
 ,则根据两点的距离公式得到|AB|=
,则根据两点的距离公式得到|AB|=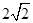 ,而求解的三角形面积的最小值即为高的最小值,那么圆心(1,0)到直线AB:y-x=2的距离
,而求解的三角形面积的最小值即为高的最小值,那么圆心(1,0)到直线AB:y-x=2的距离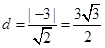 ,半径为1,故圆上点到直线AB距离的最小值为d-1,那么利用三角形的面积公式得到为
,半径为1,故圆上点到直线AB距离的最小值为d-1,那么利用三角形的面积公式得到为 ,故答案为
,故答案为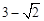


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com