
分析 求出当n≤100时,n>100时,运用等比数列的求和公式可得an,再由数列极限的运算性质,即可得到所求值.
解答 解:当n≤100时,an=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$,
当n>100时,an=3-$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=2+$\frac{1}{{2}^{n}}$.
$\underset{lim}{n→∞}$an=$\underset{lim}{n→∞}$(2+$\frac{1}{{2}^{n}}$)=2+$\underset{lim}{n→∞}$$\frac{1}{{2}^{n}}$=2+0=2.
故答案为:2.
点评 本题考查数列的极限的求法,考查等比数列的求和公式的运用,考查运算能力,属于基础题.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
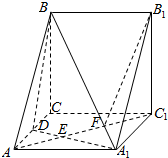 三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.
三棱柱ABC-A1B1C1中,D是AC的中点,A1D与AC1交于点E,F在线段AC1上,且AF=2FC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
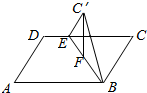 已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.
已知矩形ABCD的边长AB=6,AD=4,在CD上截取CE=4,以BE为棱将△BCE折成△BC1E,使△BC1E的高C1F⊥平面ABED,则点C1到AB的距离为2$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 180 | C. | 6$\sqrt{3}$ | D. | 6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
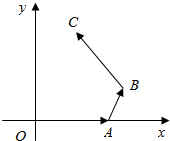 如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.
如图,在平面直角坐标系中,$|\overrightarrow{OA}|=2|\overrightarrow{AB}|=2$,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}=(-1,\sqrt{3})$,求点B,C的坐标.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {an•an+1} | B. | {nan} | C. | {${a}_{n}^{2}$} | D. | $\frac{{a}_{n}}{{a}_{n+1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com