
【题目】已知![]() .
.
(1)求函数![]() 的定义域;
的定义域;
(2)判断函数![]() 的奇偶性,并予以证明;
的奇偶性,并予以证明;
(3)求使![]() 的
的![]() 的取值范围.
的取值范围.
【答案】(1){x|1<x<1};(2)奇函数;(3)当a>1时,(0,1);当0<a<1时, (1,0).
【解析】
(1)根据对数函数的真数大于0建立关系式可求出函数的定义域;(2)判断函数f(x)-g(x)的奇偶性直接利用函数奇偶性的定义;(3)讨论a与1的大小关系,根据函数的单调性建立关系式,解之即可,需注意函数的定义域.
(1)使函数f(x)g(x)有意义,必须有:1+x>0且1x>0解得:1<x<1
所以函数f(x)g(x)的定义域是{x|1<x<1}
(2)函数f(x)g(x)是奇函数
证明:∵x∈(1,1),x∈(1,1),
f(x)g(x)=loga(1x)loga(1+x)
=[loga(1+x)loga(1x)]=[f(x)g(x)]
∴函数f(x)g(x)是奇函数
(3)使f(x)g(x)>0,即loga(1+x)>loga(1x)
当a>1时,有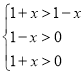 解得x的取值范围是(0,1);
解得x的取值范围是(0,1);
当0<a<1时,有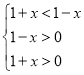 解得x的取值范围是(1,0)
解得x的取值范围是(1,0)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=2x-![]() .
.
(1)若f(x)=![]() ,求x的值;
,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二次函数![]() 的图象顶点为
的图象顶点为![]() ,且图象在
,且图象在![]() 轴上截得的线段长为8.
轴上截得的线段长为8.
(1)求函数![]() 的解析式;
的解析式;
(2)令![]() .
.
(ⅰ)求函数![]() 在
在![]() 上的最小值;
上的最小值;
(ⅱ)若![]() 时,不等式
时,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex-e-x(x∈R且e为自然对数的底数).
(1)判断函数f(x)的奇偶性与单调性.
(2)解关于t不等式f(x-t)+f(x2-2t)≥0对一切实数x都成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
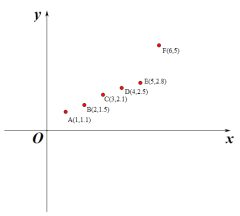
【题目】某同学将收集到的六组数据制作成散点图如图所示,并得到其回归直线的方程为![]() ,计算其相关系数为
,计算其相关系数为![]() ,相关指数为
,相关指数为![]() .经过分析确定点
.经过分析确定点![]() 为“离群点”,把它去掉后,再利用剩下的5组数据计算得到回归直线的方程为
为“离群点”,把它去掉后,再利用剩下的5组数据计算得到回归直线的方程为![]() ,相关系数为
,相关系数为![]() ,相关指数为
,相关指数为![]() .以下结论中,不正确的是
.以下结论中,不正确的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着节能减排意识深入人心,共享单车在各大城市大范围推广,越来越多的市民在出行时喜欢选择骑行共享单车.为了研究广大市民在共享单车上的使用情况,某公司在我市随机抽取了100名用户进行调查,得到如下数据:
每周使用次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)如果用户每周使用共享单车超过3次,那么认为其“喜欢骑行共享单车”.请完成下面的2×2列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否“喜欢骑行共享单车”与性别有关;
不喜欢骑行共享单车 | 喜欢骑行共享单车 | 合计 | |
男 | |||
女 | |||
合计 |
(2)每周骑行共享单车6次及6次以上的用户称为“骑行达人”,将频率视为概率,在我市所有的“骑行达人”中随机抽取4名,求抽取的这4名“骑车达人”中,既有男性又有女性的概率.
附表及公式: ,其中
,其中![]() ;
;
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当生物死亡后,其体内原有的碳14的含量大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.2019年7月6日,第43届世界遗产大会宣布,中国良渚古城遗址成功申遗,获准列入世界遗产名录.目前中国世界遗产总数已达55处,位居世界第一.今年暑期,某中学的“考古学”兴趣小组对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代学检测,检测出碳14的残留量约为初始量的54%.利用参考数据:![]() ,请你推断上述所提取的草茎遗存物距今大约有_______________________年(精确到1年).
,请你推断上述所提取的草茎遗存物距今大约有_______________________年(精确到1年).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com