
 ��tΪ���������������{an}Ϊ�ȵȲ����У�t��Ϊ�ȹ���ָ����������⣺
��tΪ���������������{an}Ϊ�ȵȲ����У�t��Ϊ�ȹ���ָ����������⣺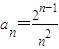 ��������{an}�DZȵȲ����У��ұȹ���
��������{an}�DZȵȲ����У��ұȹ���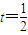 ��
��
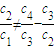 ���ʸ����в��DZȵȲ����У��ܿɾ�{an}Ϊ0�У�������{anbn}Ϊ0�У���Ȼ�����㶨�壮
���ʸ����в��DZȵȲ����У��ܿɾ�{an}Ϊ0�У�������{anbn}Ϊ0�У���Ȼ�����㶨�壮 ��Ϊ�������ʵȱ�����һ���DZȵȲ����У�
��Ϊ�������ʵȱ�����һ���DZȵȲ����У� ��Ϊ�������DZȵȲ����У�
��Ϊ�������DZȵȲ����У�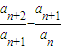 ��Ϊ�������ʲ��DZȵȲ����У��ʵȲ����в�һ���DZȵȲ����У�����ȷ��
��Ϊ�������ʲ��DZȵȲ����У��ʵȲ����в�һ���DZȵȲ����У�����ȷ�� ����
���� =
= -
- ��Ϊ������������{an}���DZȵȲ����У��ʴ���
��Ϊ������������{an}���DZȵȲ����У��ʴ��� ��
��

 ���ʸ����в��DZȵȲ����У�����ȷ��
���ʸ����в��DZȵȲ����У�����ȷ��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A���٢ڢ� | B���٢ڢ� | C���٢ڢۢ� | D���ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| a n |
| 2 |
| an+1 |
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com