
座落于我市红梅公园边的天宁宝塔堪称中华之最,也堪称佛塔世界之最.如图,已知天宁宝塔AB高度为150米,某大楼CD高度为90米,从大楼CD顶部C看天宁宝塔AB的张角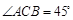 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.
180米.
解析试题分析:本题难点在于选择函数解析式模型,是用余弦定理解三角形,还是取直角三角形表示边.如用余弦定理解三角形,则得 ,解此方程成为难点;如构造直角三角形就会减少运算量,即作CE
,解此方程成为难点;如构造直角三角形就会减少运算量,即作CE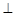 AB于E,构造直角三角形CBE和直角三角形CAE,利用两角和的正切公式得到关于BD的方程
AB于E,构造直角三角形CBE和直角三角形CAE,利用两角和的正切公式得到关于BD的方程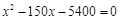 ,解此方程的运算量要少得多.将一个已知角分为两个角的和,这种思维不常见,须多加注意,深刻体会.
,解此方程的运算量要少得多.将一个已知角分为两个角的和,这种思维不常见,须多加注意,深刻体会.
试题解析:解:如图作CE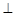 AB于E.因为AB∥CD,AB=150,CD=90,
AB于E.因为AB∥CD,AB=150,CD=90,
所以BE=90,AE=60.设CE=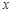 ,
, ,则
,则 . 2分
. 2分
在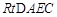 和
和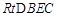 中,
中,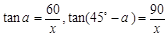 , 4分
, 4分
因为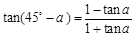 ,所以
,所以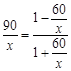 . 8分
. 8分
化简得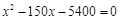 ,解得
,解得 或
或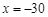 (舍去). 10分
(舍去). 10分
答:天宁宝塔AB与大楼CD底部之间的距离为180米. 12分
考点:两角和的正切公式,函数与方程.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
如图,在△ABC中,B=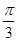 ,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.
,BC=2,点D在边AB上,AD=DC,DE⊥AC,E为垂足.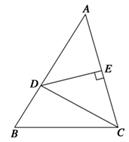
(1)若△BCD的面积为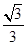 ,求CD的长;
,求CD的长;
(2)若ED=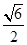 ,求角A的大小.
,求角A的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com