
【题目】以直角坐标系![]() 的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线
的原点为极点,x轴的非负半轴为极轴建立极坐标系,并且在两种坐标系中取相同的长度单位.若将曲线![]() (
(![]() 为参数)上每一点的横坐标变为原来的
为参数)上每一点的横坐标变为原来的![]() (纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为
(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C.直线l的极坐标方程为![]() .
.
(1)求曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,与x轴交于点P,线段AB的中点为M,求![]() .
.
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 为菱形,且
为菱形,且![]() ,取
,取![]() 中点为
中点为![]() .现将四边形
.现将四边形![]() 沿
沿![]() 折起至
折起至![]() ,使得
,使得![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 满足
满足![]() ,当
,当![]() 平面
平面![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,
,![]() .
.
(1)若![]() ,且点
,且点![]() 满足
满足![]() ,证明:点
,证明:点![]() 不在椭圆
不在椭圆![]() 上;
上;
(2)若椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() ,直线
,直线![]() 与线段
与线段![]() 和椭圆
和椭圆![]() 的短轴分别交于两个不同点
的短轴分别交于两个不同点![]() ,
,![]() ,且
,且![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】.对于n∈N*(n≥2),定义一个如下数阵: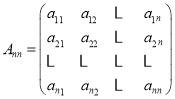 ,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设
,其中对任意的1≤i≤n,1≤j≤n,当i能整除j时,aij=1;当i不能整除j时,aij=0.设![]() .
.
(Ⅰ)当n=6时,试写出数阵A66并计算![]() ;
;
(Ⅱ)若[x]表示不超过x的最大整数,求证:![]() ;
;
(Ⅲ)若![]() ,
,![]() ,求证:g(n)﹣1<f(n)<g(n)+1.
,求证:g(n)﹣1<f(n)<g(n)+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抗击新冠肺炎的疫情中,某医院从3位女医生,5位男医生中选出4人参加援鄂医疗队,至少有一位女医生入选,其中女医生甲和男医生乙不能同时参加,则不同的选法共有种______(用数字填写答案).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花圃为提高某品种花苗质量,开展技术创新活动,在![]() 实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
实验地分别用甲、乙方法培育该品种花苗.为观测其生长情况,分别在实验地随机抽取各50株,对每株进行综合评分,将每株所得的综合评分制成如图所示的频率分布直方图,记综合评分为80分及以上的花苗为优质花苗.
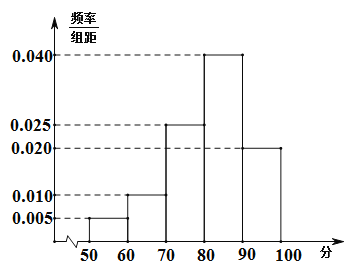
(1)用样本估计总体,以频率作为概率,若在![]() 两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
两块实验地随机抽取3株花苗,求所抽取的花苗中优质花苗数的分布列和数学期望;
(2)填写下面的列联表,并判断是否有99%的把握认为优质花苗与培育方法有关.
优质花苗 | 非优质花苗 | 合计 | |
甲培育法 | 20 | ||
乙培育法 | 10 | ||
合计 |
附:下面的临界值表仅供参考.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(参考公式: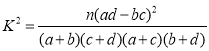 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出有关![]() 的四个论断:①
的四个论断:①![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;④
;④![]() .以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
.以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据: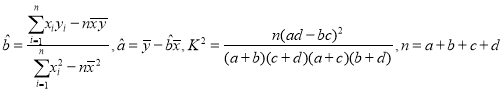 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com