
方程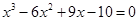 的实根个数是( )
的实根个数是( )
A.3 B.2 C.1 D.0
C
【解析】
试题分析:令f(x)=x3-6x2+9x-10,则f′(x)=3x2-12x+9=3(x-1)(x-3).
由f′(x)>0得x>3或x<1,
由f′(x)<0得1<x<3.
∴f(x)的单调增区间为(3,+∞),(-∞,1),单调减区间为(1,3),
∴f(x)在x=1处取极大值,在x=3处取极小值,
又∵f(1)=-6<0,f(3)=-10<0,
∴函数f(x)的图象与x轴有一个交点,
即方程x3-6x2+9x-10=0有一个实根.
故选C.
考点:导数的应用,方程的根,函数的零点。
点评:中档题,利用转化思想,将方程根的个数的讨论,转化成函数零点个数的讨论,通过研究函数的单调区间及极值情况,确定函数图象与x轴的交点个数。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com