
【题目】在等差数列![]() 中,
中,![]() ,前
,前![]() 项和
项和![]() 满足条件
满足条件![]() ,
,
(1)求数列![]() 的通项公式和
的通项公式和![]() ;
;
(2)记![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】下列命题正确的是__________.
①每条直线都有唯一一个倾斜角与之对应,也有唯一一个斜率与之对应;
②倾斜角的范围是:![]() ,且当倾斜角增大时,斜率不一定增大;
,且当倾斜角增大时,斜率不一定增大;
③直线![]() 过点
过点![]() ,且横截距与纵截距相等,则直线
,且横截距与纵截距相等,则直线![]() 的方程一定为
的方程一定为![]() ;
;
④过点![]() ,且斜率为1的直线的方程为
,且斜率为1的直线的方程为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是![]() ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为![]() 的正方形.
的正方形.
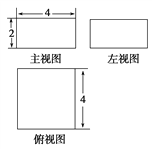
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设数列![]() 满足:
满足:
对于任意![]() ,都有
,都有![]() 成立.
成立.
①求数列![]() 的通项公式;
的通项公式;
②设数列![]() ,问:数列
,问:数列![]() 中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
中是否存在三项,使得它们构成等差数列?若存在,求出这三项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
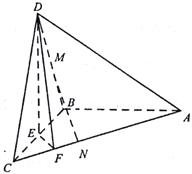
【题目】如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC的中点,F在棱AC上,且AF=3FC
(1)求三棱锥D-ABC的体积
(2)求证:平面DAC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=![]() CA,求证:MN∥平面DEF
CA,求证:MN∥平面DEF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com