
【题目】已知![]() 位数满足下列条件:①各个数字只能从集合
位数满足下列条件:①各个数字只能从集合![]() 中选取;②若其中有数字
中选取;②若其中有数字![]() ,则在
,则在![]() 的前面不含
的前面不含![]() ,将这样的
,将这样的![]() 位数的个数记为
位数的个数记为![]() ;
;
(1)求![]() 、
、![]() ;
;
(2)探究![]() 与
与![]() 之间的关系,求出数列
之间的关系,求出数列![]() 的通项公式;
的通项公式;
(3)对于每个正整数![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() 得到一个新数列
得到一个新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试探究
项和,试探究![]() 能否成立,写出你探究得到的结论并给出证明;
能否成立,写出你探究得到的结论并给出证明;
【答案】(1)![]() ,
,![]() (2)
(2)![]() ,
,![]() (3)不能成立,证明见解析
(3)不能成立,证明见解析
【解析】
(1)根据已知条件,进行分类讨论,由此计算出![]() 的值.
的值.
(2)根据已知条件,分类讨论求得![]() 和
和![]() 之间的递推关系式,由此求得数列
之间的递推关系式,由此求得数列![]() 的通项公式.
的通项公式.
(3)根据(2)中求得的数列![]() 的通项公式,计算出
的通项公式,计算出![]() ,由此证得
,由此证得![]() 不成立.
不成立.
(1)当![]() 时,这样的
时,这样的![]() 位数有
位数有![]() 个,所以
个,所以![]() .
.
当![]() 时,若个位数字为
时,若个位数字为![]() ,则十位数字可以为
,则十位数字可以为![]() ,共有
,共有![]() 种;若个位数字为
种;若个位数字为![]() ,则十位数字可以为
,则十位数字可以为![]() ,共有
,共有![]() 种.所以当
种.所以当![]() 时,共有
时,共有![]() 种,即
种,即![]() .
.
当![]() 时,若个位数字是
时,若个位数字是![]() ,则十位和百位的可能情况有
,则十位和百位的可能情况有![]() 种;若个位数字为
种;若个位数字为![]() ,则十位和百位分别有
,则十位和百位分别有![]() 种,共有
种,共有![]() 种.所以
种.所以![]() .
.
(2)结合(1)的分析可知,当![]() 位数时,若个位数字是
位数时,若个位数字是![]() ,其余
,其余![]() 个位置的方法数为
个位置的方法数为![]() ;若个位数字为
;若个位数字为![]() ,则其余
,则其余![]() 个位置的方法数为
个位置的方法数为![]() 种.所以
种.所以![]() .整理得
.整理得![]() ,所以
,所以![]() 是以
是以![]() 为首项,公差为
为首项,公差为![]() 的等差数列,则
的等差数列,则![]() ,化简得
,化简得![]() .所以数列
.所以数列![]() 的通项公式为
的通项公式为![]() .
.
(3)由(2)得![]() .则
.则
![]() ,
,
![]() ,
,
由于![]() ,所以
,所以![]() 单调递增,所以
单调递增,所以![]() 不成立.
不成立.


科目:高中数学 来源: 题型:
【题目】如图ABC﹣A1B1C1是直三棱柱,底面△ABC是等腰直角三角形,且AB=AC=4,直三棱柱的高等于4,线段B1C1的中点为D,线段BC的中点为E,线段CC1的中点为F.
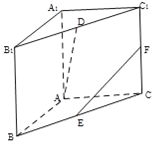
(1)求异面直线AD、EF所成角的大小;
(2)求三棱锥D﹣AEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若同时满足:
,若同时满足:
(Ⅰ)若存在闭区间![]() ,使得任取
,使得任取![]() ,都有
,都有![]() (
(![]() 是常数);
是常数);
(Ⅱ)对于![]() 内任意
内任意![]() ,当
,当![]() ,时总有
,时总有![]() 恒成立,则称函数
恒成立,则称函数![]() 为“平底型”函数.
为“平底型”函数.
(1)判断函数![]() 和
和![]() 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设![]() 是(1)中的“平底型”函数,若不等式
是(1)中的“平底型”函数,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)函数![]() 是区间
是区间![]() 上的“平底型”函数,求
上的“平底型”函数,求![]() 和
和![]() 满足的条件,并说明理由.
满足的条件,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10个不同的产品,其中4个次品,6个正品.现每次取其中一个进行测试,直到4个次品全测完为止,若最后一个次品恰好在第五次测试时被发现,则该情况出现的概率是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() 为
为![]() 阶“期待数列”:①
阶“期待数列”:①![]() ;②
;②![]() .
.
(1)若等比数列![]() 为
为![]() 阶“期待数列”
阶“期待数列”![]() ,求公比
,求公比![]() ;
;
(2)若一个等差数列![]() 既是
既是![]() 阶“期待数列”又是递增数列
阶“期待数列”又是递增数列![]() ,求该数列的通项公式;
,求该数列的通项公式;
(3)记![]() 阶“期待数列”
阶“期待数列” ![]() 的前
的前![]() 项和为
项和为![]() ,求证;数列
,求证;数列![]() 不能为
不能为![]() 阶“期待数列”.
阶“期待数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年11月18日国际射联步手枪世界杯总决赛在莆田市综合体育馆开幕,这是国际射联步手枪世界杯总决赛时隔10年再度走进中国.为了增强趣味性,并实时播报现场赛况,我校现场小记者李明和播报小记者王华设计了一套播报转码法,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的![]() 的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式:
的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数通过变换公式: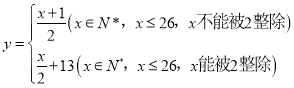 ,将明文转换成密文,如
,将明文转换成密文,如![]() ,即
,即![]() 变换成
变换成![]() ,即
,即![]() 变换成
变换成![]() .若按上述规定,若王华收到的密文是
.若按上述规定,若王华收到的密文是![]() ,那么原来的明文是( )
,那么原来的明文是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一件刚出土的珍贵文物要在博物馆大厅中央展出,需要设计各面是玻璃平面的无底正四棱柱将其罩住,罩内充满保护文物的无色气体.已知文物近似于塔形,高1.8米,体积0.5立方米,其底部是直径为0.9米的圆形,要求文物底部与玻璃罩底边至少间隔0.3米,文物顶部与玻璃罩上底面至少间隔0.2米,气体每立方米1000元,则气体费用最少为( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com