
甲和乙参加智力答题活动,活动规则:①答题过程中,若答对则继续答题;若答错则停止答题;②每人最多答3个题;③答对第一题得10分,第二题得20分,第三题得30分,答错得0分。已知甲答对每个题的概率为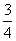 ,乙答对每个题的概率为
,乙答对每个题的概率为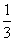 。
。
(1)求甲恰好得30分的概率;
(2)设乙的得分为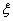 ,求
,求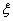 的分布列和数学期望;
的分布列和数学期望;
(3)求甲恰好比乙多30分的概率.
(1)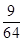
(2)分布列见解析 数学期望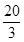
(3)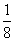
解析试题分析:(1)要求甲恰好得30分的概率,我们分析活动规则后可得,甲恰好得30分,说明甲前两题都答对,而第三题答错,代入分步事件概率公式即可得到答案.
(2)设乙的得分为ξ,则ξ的取值为0,10,30,60,我们根据活动规则,分析出ξ取不同值时的情况,代入概率公式即可求解.(3)要求甲恰好比乙多30分的概率,我们要先分析甲恰好比乙多30分的发生情况,由(2)的结论,共有两种情况,即甲恰好得30分且乙恰好得0分,或是甲恰好得60分且乙恰好得30分,代入概率公式即可求解 。
解:(I)甲恰好得30分,说明甲前两题都答对,而第三题答错,其概率为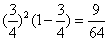 ,-------3分
,-------3分
(II)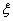 的取值为0,10, 30,60.--------4分
的取值为0,10, 30,60.--------4分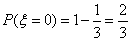 ,
,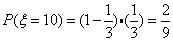
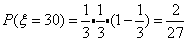 ,
,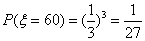
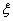 的概率分布如下表:
的概率分布如下表:
---------8分
0 10 30 60 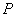

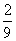
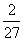
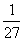
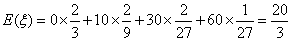 -------10分
-------10分
(III)设甲恰好比乙多30分为事件A,甲恰好得30分且乙恰好得0分为事件B1,
甲恰好得60分且乙恰好得30分为事件B2,则A=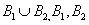 为互斥事件.
为互斥事件.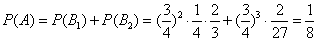 .
.
所以,甲恰好比乙多30分的概率为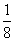 -----------14分
-----------14分
考点:本题主要考查了相互独立事件概率的计算,运用数学知识解决问题的能力。
点评:解决该试题的关键是对于要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本小题13分)已知关于x的一元二次函数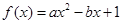 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列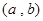 。
。
(1)若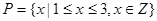 ,
,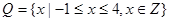 ,列举出所有的数对
,列举出所有的数对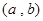 ,并求函数
,并求函数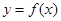 有零点的概率;
有零点的概率;
(2)若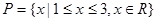 ,
,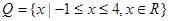 ,求函数
,求函数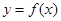 在区间
在区间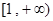 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;
(2)求至少有一次取到不合格品的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从一副扑克牌的红桃花色中取5张牌,点数分别为1、2、3、4、5,甲、乙两人玩一种游戏:
甲先取一张牌,记下点数,放回后乙再取一张牌,记下点数.如果两个点数的和为偶数就算甲胜,否则算乙胜.
(Ⅰ)求甲胜且点数的和为6的事件发生的概率;
(Ⅱ)分别求出甲胜与乙胜的概率,判断这种游戏规则公平吗?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为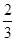 ,乙能攻克的概率为
,乙能攻克的概率为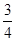 ,丙能攻克的概率为
,丙能攻克的概率为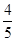 .
.
(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励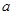 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金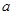 万元;若只有2人攻克,则奖金奖给此二人,每人各得
万元;若只有2人攻克,则奖金奖给此二人,每人各得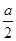 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得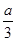 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为迎接我校110周年校庆,校友会于日前举办了一次募捐爱心演出,有1000 人参加,每人一张门票,每张100元. 在演出过程中穿插抽奖活动.第一轮抽奖从这1000张票根中随机抽取10张,其持有者获得价值1000元的奖品,并参加第二轮抽奖活动.第二轮抽奖由第一轮获奖者独立操作按钮,电脑随机产生两个数 ,满足
,满足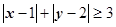 电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
电脑显示“中奖”,且抽奖者获得9000元奖金;否则电脑显示“谢谢”,则不中奖.
(1)已知校友甲在第一轮抽奖中被抽中,求校友甲在第二轮抽奖中获奖的概率;
(2)若校友乙参加了此次活动,求校友乙参加此次活动收益的期望;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为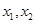 ,记
,记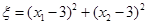 .
.
(1)分别求出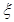 取得最大值和最小值时的概率; (2)求
取得最大值和最小值时的概率; (2)求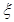 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)一只口袋内装有大小相同的5只球,其中3只白球,2只黑球.现从口袋中每次任取一球,每次取出不放回,连续取两次.问:
(1)取出的两只球都是白球的概率是多少?
(2)取出的两只球至少有一个白球的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中装有标号为1,2,3,4的4张标签,随机地选取两张标签,根据下列条件求两张标签上的数字为相邻整数的概率:
(1) 标签的选取是无放回的; (2) 标签的选取是有放回的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com