
分析 利用复数代数形式的乘法运算展开并化简,再由复数的模等于12列式求得a值.
解答 解:z=$\sqrt{2}$i(1+i)3(a-i)2=$\sqrt{2}i(-2+2i)({a}^{2}-1-2ai)$=$-2\sqrt{2}[({a}^{2}-1+2a)+({a}^{2}-1-2a)i]$,
由题意可知,|z|=$2\sqrt{2}\sqrt{({a}^{2}-1+2a)^{2}+({a}^{2}-1-2a)^{2}}=12$,
整理得:${a}^{2}=3\sqrt{2}-1$,
∴$a=±\sqrt{3\sqrt{2}-1}$.
故答案为:$±\sqrt{3\sqrt{2}-1}$.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.


科目:高中数学 来源: 题型:解答题
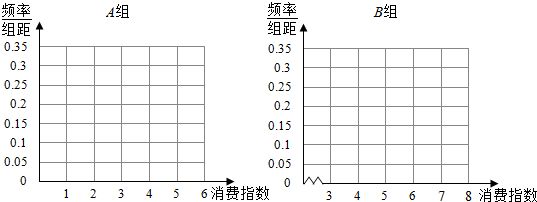
| 消费指数(百元) | [1,2) | [2,3) | [3,4) | [4,5) | [5,6) |
| 人数 | 3 | 4 | 6 | 5 | 2 |
| 消费指数(百元) | [3,4) | [4,5) | [5,6) | [6,7) | [7,8] |
| 人数 | 9 | 36 | a | 54 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | 2或$\frac{1}{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
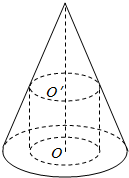 如图,圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′,下底面在圆锥SO的底面上,设圆柱OO′的体积为V1,圆锥SO的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$.
如图,圆锥SO的内接圆柱OO′的上底面经过高SO的中点O′,下底面在圆锥SO的底面上,设圆柱OO′的体积为V1,圆锥SO的体积为V2,则$\frac{{V}_{1}}{{V}_{2}}$=$\frac{3}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | ±4$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com