
【题目】已知中心在坐标原点![]() ,一个焦点为
,一个焦点为![]() 的椭圆被直线
的椭圆被直线![]() 截得的弦的中点的横坐标为
截得的弦的中点的横坐标为![]() .
.
(1)求此椭圆的方程;
(2)设直线![]() 与椭圆交于
与椭圆交于![]() 两点,且以
两点,且以![]() 为对角线的菱形的一个顶点为
为对角线的菱形的一个顶点为![]() ,求
,求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)最大值1,
(2)最大值1, ![]()
【解析】【试题分析】(1)依题意可知![]() ,得到
,得到![]() ,设出
,设出![]() 两点的坐标,利用点差法可得到
两点的坐标,利用点差法可得到![]() 的另一个关系式
的另一个关系式![]() ,由此求得
,由此求得![]() 的值.(2)联立直线的方程和椭圆的方程,消去
的值.(2)联立直线的方程和椭圆的方程,消去![]() 写出韦达定理,利用菱形和椭圆的弦长公式,求得
写出韦达定理,利用菱形和椭圆的弦长公式,求得![]() 面积的表达式,在利用二次函数最值来求得面积的最大值.
面积的表达式,在利用二次函数最值来求得面积的最大值.
【试题解析】
(1)设所求椭圆方程为![]() ,由题意知
,由题意知![]() ,①
,①
设直线与椭圆的两个交点为![]() ,弦
,弦![]() 的中点为
的中点为![]() ,
,
由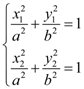 ,两式相减得:
,两式相减得:![]() ,
,
两边同除以![]() ,得
,得![]() ,即
,即![]() .
.
因为椭圆被直线![]() 截得的弦的中点
截得的弦的中点![]() 的横坐标为
的横坐标为![]() ,所以
,所以![]()
![]() ,
,
所以![]() ,
, ![]() ,所以
,所以![]() ,即
,即![]() ,②
,②
由①②可得![]() ,
,
所以所求椭圆的方程为![]() .
.
(2)设![]() ,
, ![]() 的中点为
的中点为![]() ,
,
联立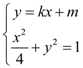 ,消
,消![]() 可得:
可得: ![]() ,
,
此时![]() ,即
,即![]() ①
①
又![]() ,
,![]() ,
,
![]() 为对角线的菱形的一顶点为
为对角线的菱形的一顶点为![]() ,由题意可知
,由题意可知![]() ,即
,即![]()
整理可得: ![]() ②
②
由①②可得![]() ,
,![]() ,
,
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则
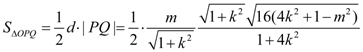
![]() ,
,
当![]() 的面积取最大值1,此时
的面积取最大值1,此时![]()
![]()
∴直线方程为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】信息科技的进步和互联网商业模式的兴起,全方位地改变了大家金融消费的习惯和金融交易模式,现在银行的大部分业务都可以通过智能终端设备完成,多家银行职员人数在悄然减少.某银行现有职员320人,平均每人每年可创利20万元.据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.2万元,但银行需付下岗职员每人每年6万元的生活费,并且该银行正常运转所需人数不得小于现有职员的![]() ,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
,为使裁员后获得的经济效益最大,该银行应裁员多少人?此时银行所获得的最大经济效益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面为等腰梯形,且底面与侧面
中,底面为等腰梯形,且底面与侧面![]() 垂直,
垂直, ![]() ,
, ![]() 分别为线段
分别为线段![]() 的中点,
的中点, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() .
.

(1)证明: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人租用一块土地种植一种瓜类作物,租期5年,根据以往的年产量数据,得到年产量频率分布直方图如图所示,以各区间中点值作为该区间的年产量,得到平均年产量为455kg.当年产量低于450kg时,单位售价为12元/kg,当年产量不低于450kg时,单位售价为10元/kg. 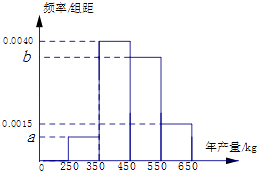
(1)求图中a的值;
(2)以各区间中点值作为该区间的年产量,并以年产量落入该区间的频率作为年产量取该区间中点值的概率,求年销售额X(单位:元)的分布列;
(3)求在租期5年中,至少有2年的年销售额不低于5000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 且点(4,2)在函数f(x)的图象上.
且点(4,2)在函数f(x)的图象上.
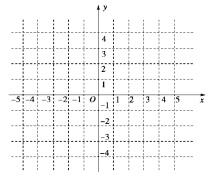
(1)求函数f(x)的解析式,并在图中的直角坐标系中画出函数f(x)的图象;
(2)求不等式f(x)<1的解集;
(3)若方程f(x)-2m=0有两个不相等的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知圆C1:x2+y2=4,圆C2:(x﹣2)2+y2=4.
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别求圆C1与圆C2的极坐标方程及两圆交点的极坐标;
(2)求圆C1与圆C2的公共弦的参数方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com