
【题目】如图所示,四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,△ABC为等腰三角形,
,△ABC为等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.![]()

(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)连结PF,先证明DC⊥平面ABC,再证明AFPE是平行四边形,得到EP⊥平面BCD
(Ⅱ)先得到EP是三棱锥E﹣BDF的高,再计算EP=![]() ,代入面积公式计算得到答案.
,代入面积公式计算得到答案.
(I)由题意知△ABC为等腰直角三角形,
而F为BC的中点,所以AF⊥BC.
又因为平面AEDC⊥平面ABC,且∠ACD=90°,
所以DC⊥平面ABC.
而AF平面ABC,所以AF⊥DC.
而BC∩DC=C,所以AF⊥平面BCD.
连结PF,则PF∥DC,PF=![]() DC,
DC,
而AE∥DC,AE=![]() DC,所以AE∥PF,AE=PF,
DC,所以AE∥PF,AE=PF,
AFPE是平行四边形,
因此EP∥AF,故EP⊥平面BCD.

(II)因为EP⊥平面BCD,所以EP⊥平面BDF,EP是三棱锥E﹣BDF的高.
所以EP=AF=![]() BC=
BC=![]() =
=![]() .
.
故三棱锥E﹣BDF的体积为:
V=![]() .
.


 培优三好生系列答案
培优三好生系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,PO垂直于圆O所在的平面,且PO=OB=1.
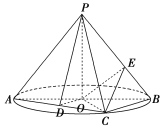
(1)若D为线段AC的中点,求证:AC⊥平面PDO;
(2)求三棱锥P-ABC体积的最大值;
(3)若![]() ,点E在线段PB上,求CE+OE的最小值.
,点E在线段PB上,求CE+OE的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,AB=BC=2,P为AB边上一动点,PD∥BC交AC于点D,现将△PDA沿PD翻折至△PDA1,E是A1C的中点.
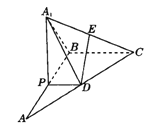
(1)若P为AB的中点证明:DE∥平面PBA1.
(2)若平面PDA1⊥平面PDA,且DE⊥平面CBA1,求二面角P﹣A1D﹣C的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,等比数列{bn}的前n项和为Tn,a1=﹣1,b1=1,a2+b2=2.
(1)若a3+b3=5,求{bn}的通项公式;
(2)若T3=21,求S3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
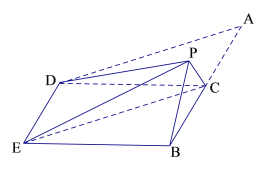
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com