
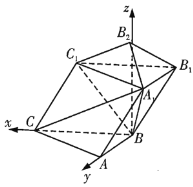
【题目】如图,在三棱柱![]() 中,
中,![]() ,侧面
,侧面![]() 为矩形,
为矩形,![]() .将
.将![]() 绕
绕![]() 翻折至
翻折至![]() ,使
,使![]() 在平面
在平面![]() 内.
内.
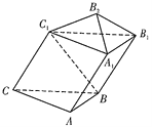
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]() .
.
【解析】
(1)根据题意证明![]() ,
,![]() ,可以得到平面
,可以得到平面![]() 平面
平面![]() ,再由
,再由![]() 平面
平面![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)易知![]() ,直线
,直线![]() 与平面
与平面![]() 所成角即直线
所成角即直线![]() 与平面
与平面![]() 所成角,建立空间直角坐标系,求出
所成角,建立空间直角坐标系,求出![]() 和平面
和平面![]() 的一个法向量,即可求解.
的一个法向量,即可求解.
(1)如图,连接![]() ,记
,记![]() ,
,
因为![]() ,所以四边形
,所以四边形![]() 为菱形,
为菱形,
又![]() ,所以
,所以![]() ,
,
则![]() ,
,![]() ,
,
由![]() ,
,![]() ,知
,知![]() ,
,
故![]() ,故
,故![]() ,又
,又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() ,同理
,同理![]() 平面
平面![]() ,且
,且
![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
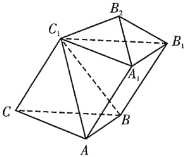
(2)连接![]() ,则
,则![]() ,易知
,易知![]() ,
,
∴直线![]() 与平面
与平面![]() 所成角即直线
所成角即直线![]() 与平面
与平面![]() 所成角.
所成角.
以![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 所在的直线为
所在的直线为![]() 轴,
轴,
过![]() 且与平面
且与平面![]() 垂直的直线为
垂直的直线为![]() 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,设
,设![]() ,
,
由题意知![]() ,
,![]() ,故
,故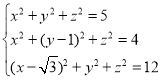 ,
,
则 ,
,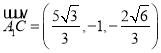 .
.
设平面![]() 法向量为
法向量为![]() ,
,
则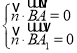 ,即
,即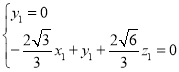 ,取
,取![]() ,
,
∴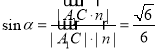 (
(![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角),
所成的角),
即直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】惰性气体分子为单原子分子,在自由原子情形下,其电子电荷分布是球对称的.负电荷中心与原子核重合,但如两个原子接近,则彼此能因静电作用产生极化(正负电荷中心不重合),从而导致有相互作用力,这称为范德瓦尔斯相互作用.今有两个相同的惰性气体原子,它们的原子核固定,原子核正电荷的电荷量为![]() ,这两个相距为
,这两个相距为![]() 的惰性气体原子组成体系的能量中有静电相互作用能
的惰性气体原子组成体系的能量中有静电相互作用能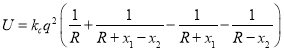 ,其中
,其中![]() 为静电常量,
为静电常量,![]() ,
,![]() 分别表示两个原子负电中心相对各自原子核的位移,且
分别表示两个原子负电中心相对各自原子核的位移,且![]() 和
和![]() 都远小于
都远小于![]() ,当
,当![]() 远小于1时,
远小于1时,![]() ,则
,则![]() 的近似值为( )
的近似值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在四棱柱ABCD—A1B1C1D1中,底面ABCD是菱形,且平面A1ADD1⊥平面ABCD,DA1=DD1,点E,F分别为线段A1D1,BC的中点.
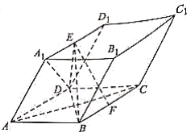
(1)求证:EF∥平面CC1D1D;
(2)求证:AC⊥平面EBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某“双一流A类”大学就业部从该校2018年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在人民币1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率分布直方图:

(1)为感谢同学们对这项调查工作的支持,该校利用分层抽样的方法从样本的前两组中抽出6人,各赠送一份礼品,并从这6人中再抽取2人,各赠送某款智能手机1部,求获赠智能手机的2人月薪都不低于1.75万元的概率;
(2)同一组数据用该区间的中点值作代表.
(i)求这100人月薪收入的样本平均数![]() 和样本方差
和样本方差![]() ;
;
(ii)该校在某地区就业的2018届本科毕业生共50人,决定于2019国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设![]() ,月薪落在区间
,月薪落在区间![]() 左侧的每人收取400元,月薪落在区间
左侧的每人收取400元,月薪落在区间![]() 内的每人收到600元,月薪落在区间
内的每人收到600元,月薪落在区间![]() 右侧的每人收取800元.
右侧的每人收取800元.
方案二:按每人一个月薪水的3%收取;用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用?
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别是椭圆
分别是椭圆![]()
![]() 的左顶点和上顶点,
的左顶点和上顶点,![]() 为其右焦点,
为其右焦点,![]() ,且该椭圆的离心率为
,且该椭圆的离心率为![]() ;
;
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆上的一动点,且不与椭圆顶点重合,点
为椭圆上的一动点,且不与椭圆顶点重合,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,线段
轴的交点,线段![]() 的中垂线与
的中垂线与![]() 轴交于点
轴交于点![]() ,若直线
,若直线![]() 斜率为
斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() (
(![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某玩具厂拟定生产两款新毛绒玩具样品,一款为毛绒小猪,另一款为毛绒小狗.由设计图知,生产这两款毛绒玩具均需相同材质的填充物、长毛绒、天鹅绒,且每个毛绒小猪需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,每个毛绒小狗需填充物
,每个毛绒小狗需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() .现有所需填充物
.现有所需填充物![]() 、长毛绒
、长毛绒![]() 、天鹅绒
、天鹅绒![]() ,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
,若每个毛绒小猪与毛绒小狗的出厂价分别为64元、36元,则生这批毛绒玩具的最大销售额为_______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,由于疫情影响,开学延迟,为了不影响学生的学习,国务院、省市区教育行政部门倡导各校开展“停学不停课、停学不停教”,某校语文学科安排学生学习内容包含老师推送文本资料学习和视频资料学习两类,且这两类学习互不影响已知其积分规则如下:每阅读一篇文本资料积1分,每日上限积5分;观看视频1个积2分,每日上限积6分.经过抽样统计发现,文本资料学习积分的概率分布表如表1所示,视频资料学习积分的概率分布表如表2所示.


(1)现随机抽取1人了解学习情况,求其每日学习积分不低于9分的概率;
(2)现随机抽取3人了解学习情况,设积分不低于9分的人数为ξ,求ξ的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线E的极坐标方程为![]() ,直线l的参数方程为
,直线l的参数方程为![]() (t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(t为参数).点P为曲线E上的动点,点Q为线段OP的中点.
(1)求点Q的轨迹(曲线C)的直角坐标方程;
(2)若直线l交曲线C于A,B两点,点![]() 恰好为线段AB的三等分点,求直线l的普通方程.
恰好为线段AB的三等分点,求直线l的普通方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com